算法
查找
二分查找
def binsearch(arr, target):
low, high = 0, len(arr)-1
while low <= high:
mid = (low + high) // 2
if target == arr[mid]:
return mid
elif target > arr[mid]:
low = mid + 1
else:
high = mid - 1
return -1
排序
冒泡
"""
冒泡排序:每趟能确定一个元素的最终位置
"""
def bubble_sort(data):
n = len(data)
for i in range(n-1):
for j in range(n-i-1):
if data[j] > data[j+1]:
data[j], data[j+1] = data[j+1], data[j]
print(data)
快排
def quick_sort(arr):
# 用栈保存区间左右边界,右边界先入栈
stack = [len(arr)-1, 0]
while stack:
low, high = stack.pop(), stack.pop()
p = partition(arr, low, high)
# 基准元素的左区间存在则入栈
if p > low:
stack.append(p - 1)
stack.append(low)
# 基准元素的右区间存在则入栈
if high > p:
stack.append(high)
stack.append(p + 1)
return arr
def partition(arr, low, high):
# 选取第一个元素作为基准元素
p = arr[low]
while low < high:
# 比基准元素小的移到前面
while low < high and arr[high] >= p:
high -= 1
arr[low] = arr[high]
# 比基准元素大的移到后面
while low < high and arr[low] <= p:
low += 1
arr[high] = arr[low]
# 将基准元素放到最终的位置
arr[low] = p
return low
选择
"""
选择排序:每趟(i)从后面的n-i+1个待排元素选择1个最小的作为最终第i个元素的值
"""
def select_sort(arr):
n = len(arr)
for i in range(n-1):
min = i
for j in range(i+1, n):
if arr[j] < arr[min]:
min = j
# 若第一个数字不是最小值,则交换位置
if min != i:
arr[i], arr[min] = arr[min], arr[i]
return arr
归并
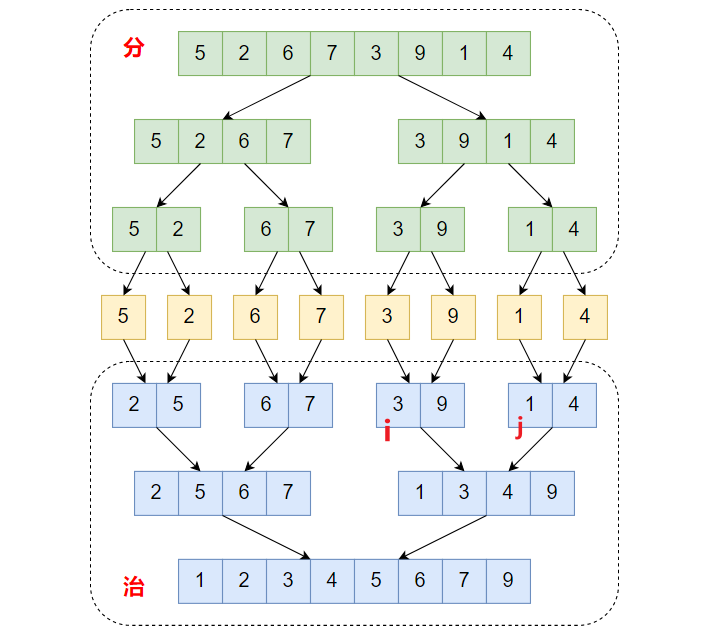
==思路==:
- 针对上图序列A(3,9)和序列B(1,4),指针i指向3,j指向1
- 1 < 3,1添加到temp,同时指针j后移
- 3 < 4,3添加到temp,同时指针i后移
- 4 < 9,4添加到temp,同时指针j后移,此时j=8 > 右边界r=7,跳出循环
- 此时i=5,j=8,mid=5,l=4,r=7,将剩下的序列A中的元素添加到temp列表中
- 将temp中的所有元素赋给原序列arr对应位置
def merge(arr, l, r, mid):
temp = []
i, j = l, mid + 1
while i <= mid and j <= r:
if arr[i] < arr[j]:
temp.append(arr[i])
i += 1
else:
temp.append(arr[j])
j += 1
print('-----------')
print(f'i:{i} j:{j} mid:{mid} l:{l} r:{r}')
# 此时其中一序列(如1,3,4)已经全部按顺序添加到temp中,另一序列还剩9,只需将剩下的添加到temp
while i <= mid:
temp.append(arr[i])
i += 1
while j <= r:
temp.append(arr[j])
j += 1
print(temp)
# 此时子序列已排好序,直接将temp中排好序的元素赋给arr对应位置
arr[l: r + 1] = temp
print(arr)
def merge_sort(arr, l, r):
if l < r:
mid = (l+r) // 2
merge_sort(arr, l, mid)
merge_sort(arr, mid+1, r)
merge(arr, l, r, mid)
return arr
基础
查找第一个不重复的字符
def first_char(arr):
d = {}
"""记录每个字符的出现次数"""
for i, v in enumerate(arr):
if v in d:
d[v] += 1
else:
d[v] = 1
print(d)
"""再次遍历返回次数为1的元素"""
for i, v in enumerate(arr):
if d[v] == 1:
return v
print(first_char(['a', 'b', 'c', 'c', 'c', 'd', 'e', 'f', 'a']))
动态规划
01背包问题
从n个物品中选取一些物品(物品下标为i,背包容量为j),使得容量为s的背包包含的物品总价值最大。
# 使用滚动数组优化:
# dp[j]表示容量为j的背包所装的最大价值
dp[j] = max(dp[j], dp[j-w[i]]+v[i])
def backpack():
# 使用滚动数组dp[j]取代二维数组,表示容量为j的背包所装的最大价值
w = [2, 3, 4, 6, 5] # 重量
v = [4, 5, 3, 3, 6] # 价值
s = 8 # 最大承受重量
n = len(w) # 物品个数
dp = [0] * (s+1)
obj_list = []
dp1 = [[0]*(s+1) for i in range(n+1)]
# 二维数组方法
for i in range(1, n+1):
for j in range(s+1):
if j >= w[i-1]:
dp1[i][j] = max(dp1[i-1][j], dp1[i-1][j-w[i-1]] + v[i-1])
else:
dp1[i][j] = dp1[i-1][j]
print(dp1[-1])
# 一维滚动数组
for i in range(n):
for j in range(s, w[i]-1, -1): # 倒序遍历背包
dp[j] = max(dp[j], dp[j-w[i]] + v[i])
return dp
礼物最大价值
在一个 m*n 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于 0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物?
链接:https://leetcode.cn/problems/li-wu-de-zui-da-jie-zhi-lcof
def maxValue(grid: List[List[int]]) -> int:
width = len(grid[0])
height = len(grid)
dp = [[0]*(width+1) for _ in range(height+1)]
# 注意遍历顺序需要和i,j对应
for i in range(1, height+1):
for j in range(1, width+1):
dp[i][j] = max(dp[i-1][j], dp[i][j-1]) + grid[i-1][j-1]
return dp[height][width]
maxValue([[1,2,5],[3,2,1]])
滑动窗口
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。返回滑动窗口中的最大值 。 链接:https://leetcode.cn/problems/sliding-window-maximum
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3 输出:[3,3,5,5,6,7] 解释: 滑动窗口的位置 最大值
[1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7
def maxSlidingWindow(nums: List[int], k: int) -> List[int]:
# 双端队列
q = collections.deque
res = []
for i in range(len(nums)):
# 单调递减栈
while q and nums[i] >= nums[q[-1]]:
q.pop()
q.append(i)
# # 当队头元素超出窗口边界时,弹出队头元素
while q[0] <= i-k:
q.popleft()
# 从第二个窗口开始之后都要弹出队头元素,第一个窗口右边界k-1
if i>=k-1:
res.append(nums[q[0]])
return res
数组和树形数据转换
data = [
{'id': 1, 'pid': 0},
{'id': 2, 'pid': 1},
{'id': 7, 'pid': 2},
{'id': 8, 'pid': 6}
]
-
扁平数组树形化
def list2Tree(data, parent=None):
output = []
for node in data:
if node["pid"] != parent:
continue
children = list2Tree(data, node["id"])
node.update(children=children)
output.append(node)
return output -
树形数据扁平化
def flat_tree(data):
ret = []
for item in data:
ret.append({"id": item["id"], "pid": item["pid"]})
if item.get("children"):
ret.extend(flat_tree(item["children"]))
return ret
最大数字组合
有几个任意位数的正整数,求能组成的最大数字
思路:
若 a+b > b+a,则a应该在前,否则a在后
from functools import cmp_to_key
def max_number(nums):
# 自定义比较函数
def compare(x, y):
# 将两个字符串拼接起来进行比较
return int(y + x) - int(x + y)
# 将正整数转换为字符串
nums = [str(num) for num in nums]
# 使用自定义的比较函数对字符串进行排序
nums.sort(key=cmp_to_key(compare))
# 将排序后的字符串连接起来得到最大数
result = ''.join(nums)
return result
MySQL
基础
1 #DISTINCT返回唯一不同的值
SELECT DISTINCT 列名称 FROM 表名称
2#ORDER BY排序(DESC降序,ASC升序)
SELECT Company, OrderNumber FROM Orders ORDER BY Company DESC, OrderNumber ASC
3# IFNULL如果第一个参数 为 NULL,则返回第二个参数的备用值
IFNULL(
(SELECT DISTINCT Salary
FROM Employee
ORDER BY Salary DESC
LIMIT 2 OFFSET 1), #返回从第三行开始,共1行数据
NULL)
)
4 #join内连接,和inner join效果一样
SELECT a.NAME AS Employee
FROM Employee AS a JOIN Employee AS b
ON a.ManagerId = b.Id
AND a.Salary > b.Salary
5# Dense_RANK() over对成绩排名,RANK() over排名时若有并列将占用下一位的位置
select Score,Dense_RANK() over (order by Score desc) as `Rank`
from Scores
6 #顺序:where——group by——having,注意group by紧跟在where最后一个限制条件后面,不能被夹在where限制条件之间。使用了having必须使用group by,但是使用group by 不一定使用having
7 #IF(condition, value_if_true, value_if_false)
8#回购率:某一个时间窗口内消费的用户,在下一个时间窗口仍旧消费的占比
#复购率:在某时间窗口内重复消费用户(消费两次及以上的用户)在总消费用户中占比
次日留存率
#查看用户在某天刷题后第二天还会再来刷题的平均概率。
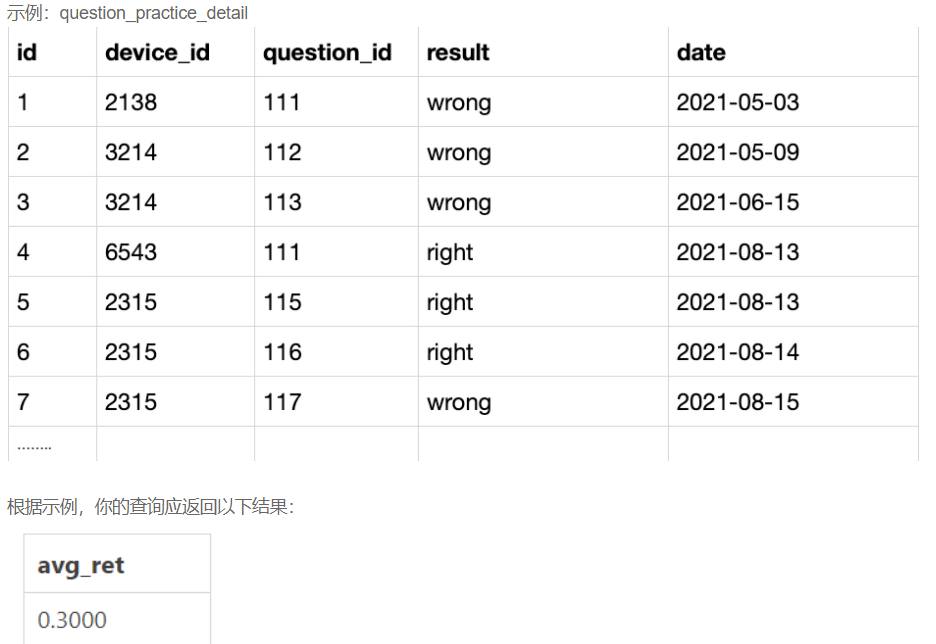
#先对用户去重,然后自连接,q1显示所有,q2显示留存
select
count(q2.device_id)/count(q1.device_id) as avg_ret
from
(select distinct device_id, date from question_practice_detail) q1
left join
(select distinct device_id, date from question_practice_detail) q2
on q1.device_id=q2.device_id and q2.date=date_add(q1.date,interval 1 day)