import TOCInline from '@theme/TOCInline'
一元函数微积分
微分学
函数 极限 连续
一、 函数
考点:1)、函数有界性、单调性、周期性、奇偶性的判定
2)、复合函数
1、函数概念
基本要素:定义域、对应法则
2、常用函数
符号函数 y=sgnx
取整函数 y=[x] (不超过x的最大整数)
3、复合函数

不是任意两个函数都可以复合
4、反函数

不是任意两个函数都有反函数
单调函数=>反函数
有反函数<=>对定义域中的任意x1、x2,有f(x1)不等于f(x2)
f^-1^[f(x)]=f[f^-1^(x)]=x
5、初等函数
定义:由常数和基本初等函数经过有限次加减乘除和复��合所得到的只能用一个解析式表示的函数
基本初等函数:幂函数、指数、对数、三角、反三角
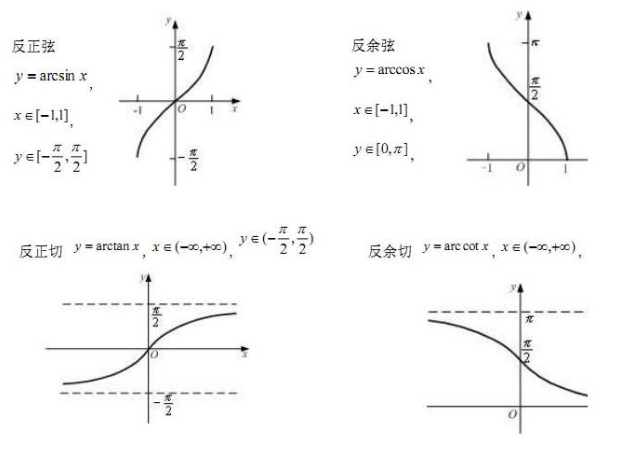
6、函数的性质
1)、单调性

2)、奇偶性
奇+奇=奇、偶+偶=偶、奇×奇=偶、 奇×偶=奇

3)、周期性
f(x)周期为T,则f(ax+b)周期为T/|a|

4)、有界性
有界函数:若存在M>0,使得对任意的x$\epsilon$X,恒有|f(x)|<=M
无界函数:对任意的M>0,至少存在一个x
0$\epsilon$X,使得|f(x0)|>M

————强化题型




积分中值定理或定积分不等式均可
二、极限
考点:
1)、极限的概念性质及存在准则
2)、求极限
3)、无穷小量阶的比较
1、数列极限

2、函数极限





极限性质:

如:f(x)=x²,g(x)=x³在x=0处
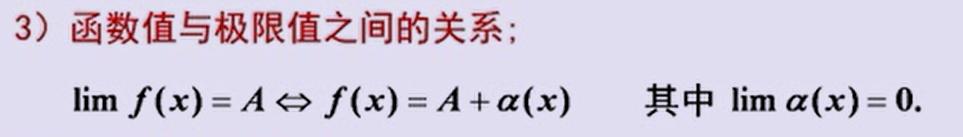
3、极限存在准则

夹逼准则的应用:
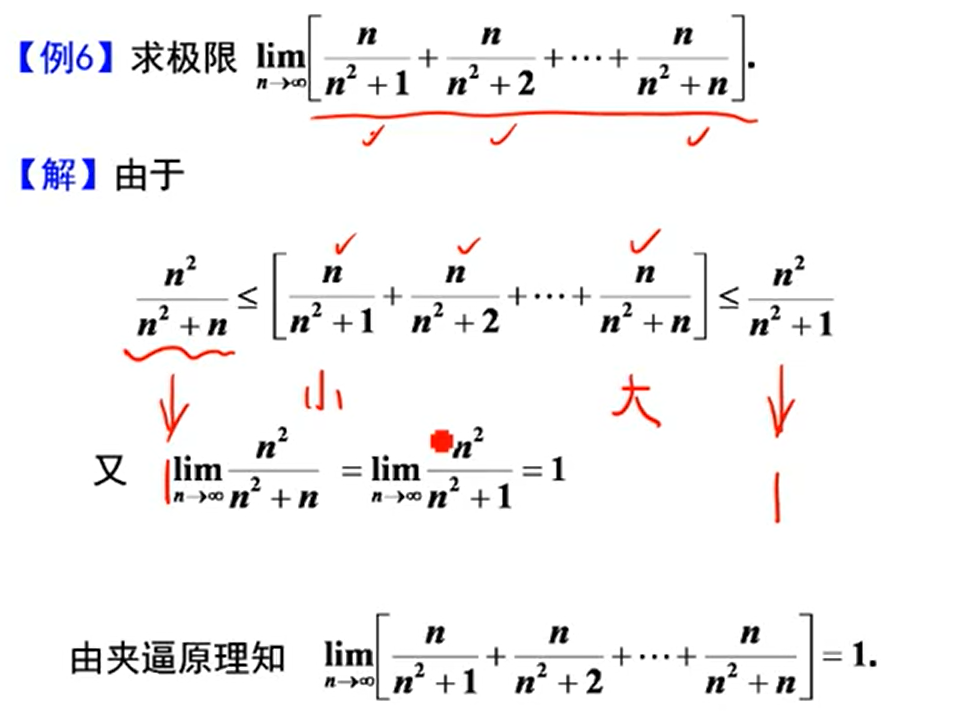
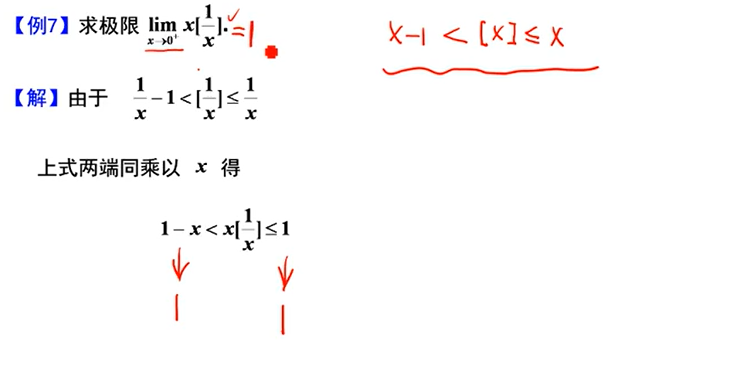
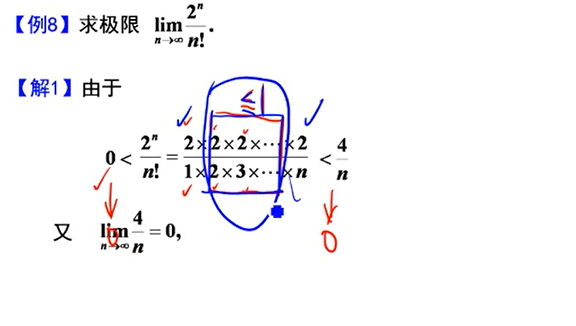
4、无穷小量(极限为0的变量)


无穷小量的应用:

5、无穷大量

无穷大量的性质
(1)**有限****个无穷大量的积仍为无穷大量;
(2)无穷大量与有界变量之和仍为无穷大量;
无穷大量与无界变量的关系



选C,考查对极限概念的理解,两式中的ε可以不相等,而不能片面理解成两个ε的值相等,如果只靠背公式则会出错

选D,D选项条件中不能包含所有的序列,还缺少X3n+2项,ABC都包含了所有项

6、求极限常用方法



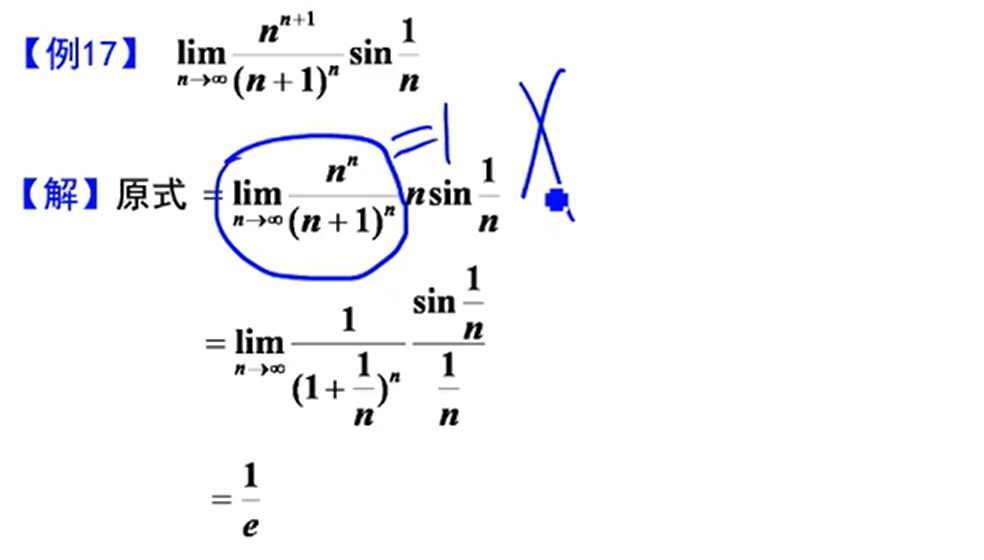
容易犯经典错误

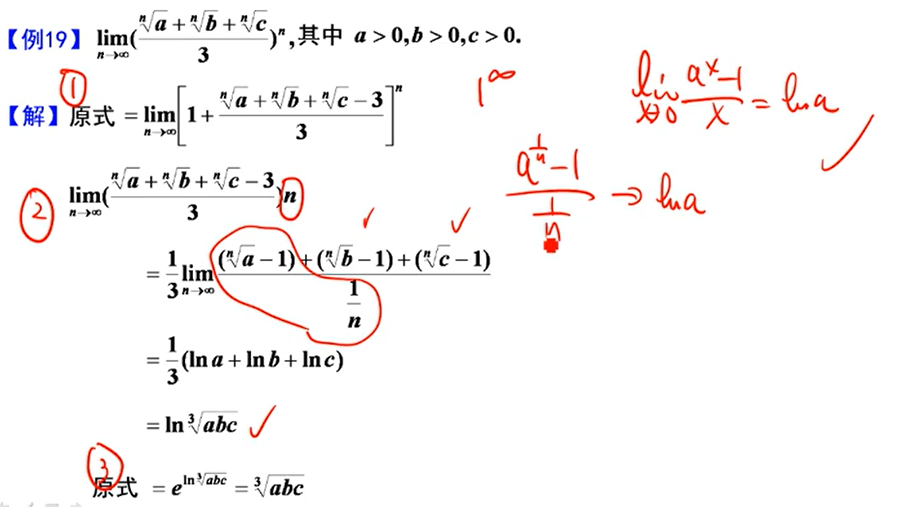


常用等价无穷小

等价无穷小(1+x)^n^-1~nx

也可直接用洛必达法则


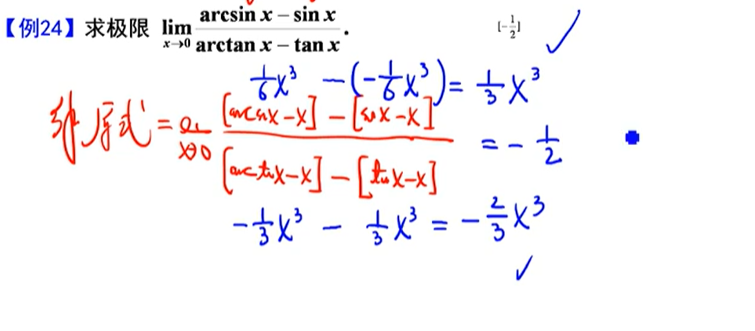


极限 、连续、导数、级数均满足以上性质

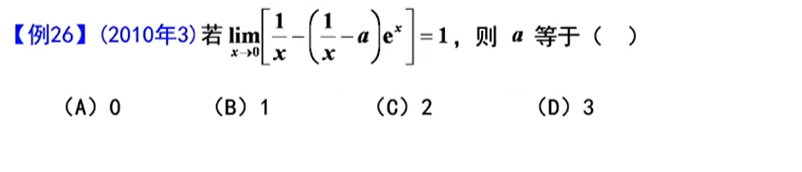
将其内部分解,利用有理运算相加减法则



洛必达法则

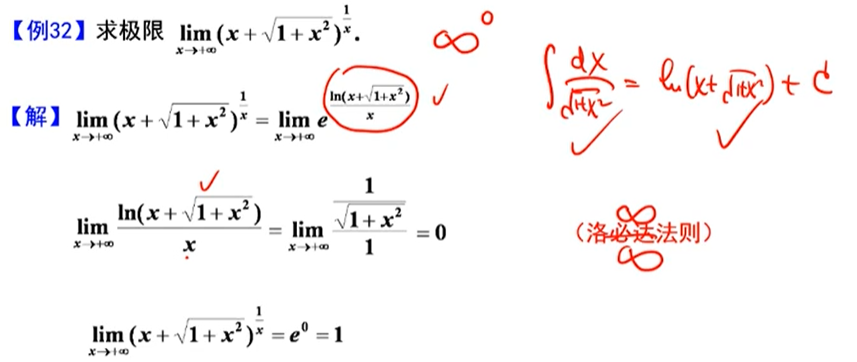
先变换成洛必达法则适用形式

此题易犯错,如果告诉f(x)n阶可导,则洛必达法则只能用到(n-1)阶,除非条件为连续可导
泰勒公式

带佩亚诺余项的公式用于求极限、极值;拉格朗日用于求最值、不等式
常用的泰勒公式
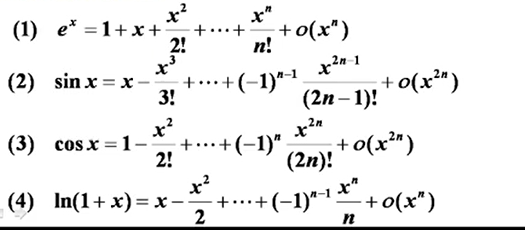
展开原则:
1、分式上下同阶原则(A/B形式):将分子分母展开到同阶
2、加减幂次最低原则(A-B形式):将A、B展开到它们系数不相等的x的最低次幂为止(即幂次数相同,且幂次数是第一次出现,其系数也不同)
若α ~ β $\Longrightarrow$α=β+o(β) $$ (tanx-x)~ \sim \frac{1}{3}x^3,\Longrightarrow tanx=x+\frac{1}{3}x^3+o(x^3) $$
$$ (x-arctanx)~ \sim \frac{1}{3}x^3,\Longrightarrow arctanx=x-\frac{1}{3}x^3+o(x^3) $$
$$ (arcsinx-x)~ \sim \frac{1}{6}x^3,\Longrightarrow arcsinx=x+\frac{1}{6}x^3+o(x^3) $$
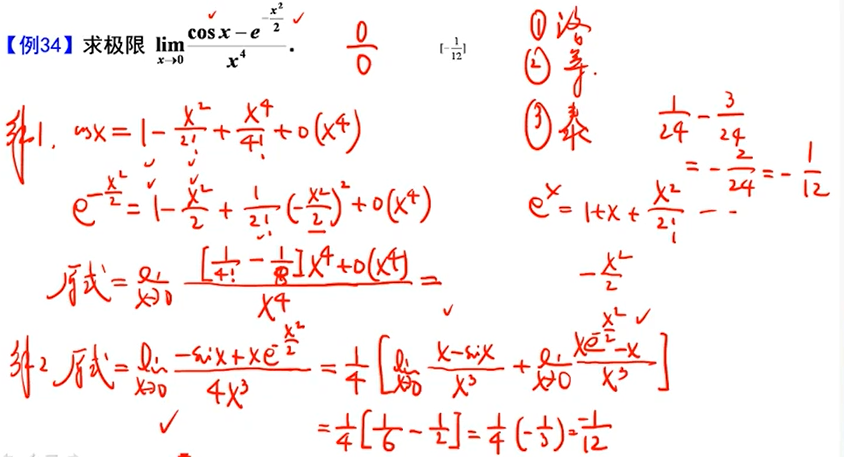
解法一为泰勒,解法二为洛必达+等价无穷小
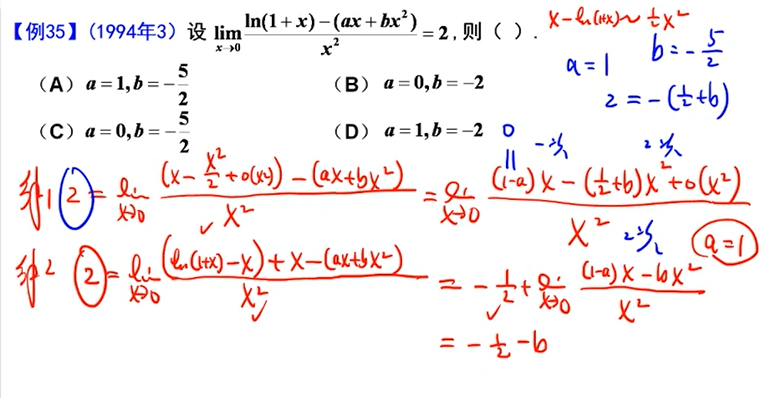
解法一泰勒展开,利用x-ln(1+x)等价于1/2x^2^求解(其中一次项系数必须等于0,否则极限不存在

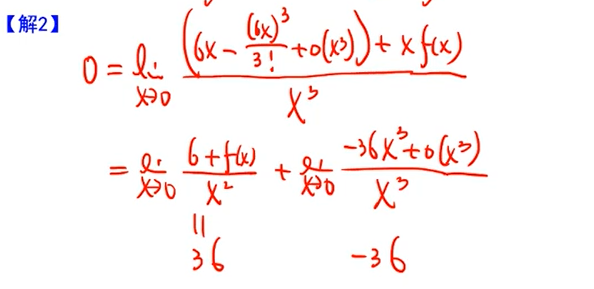
将左式拼接成右式
夹逼原理
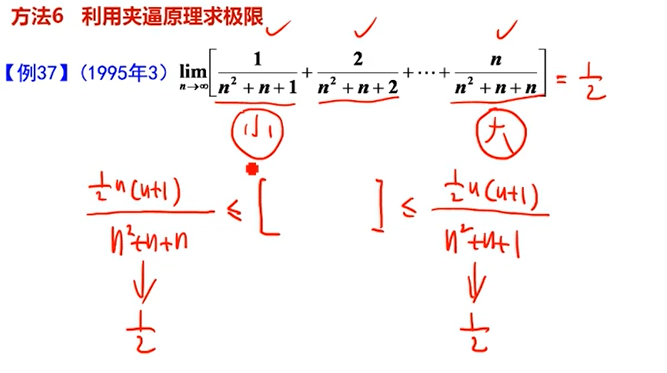
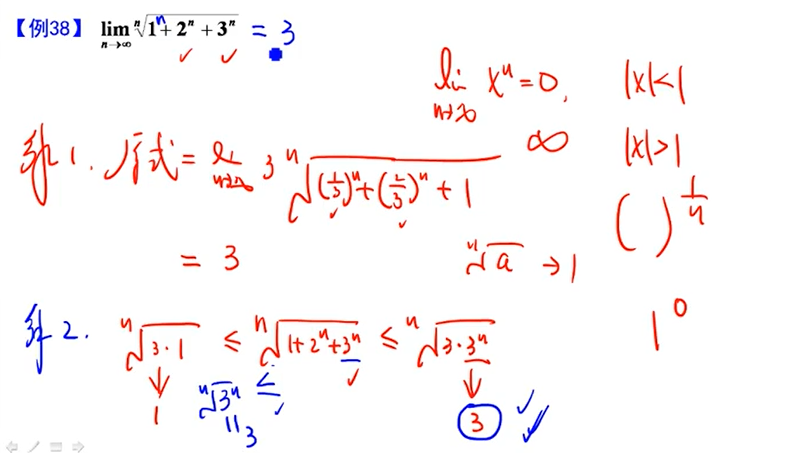


常用结论根号下的式子中,1/a最大
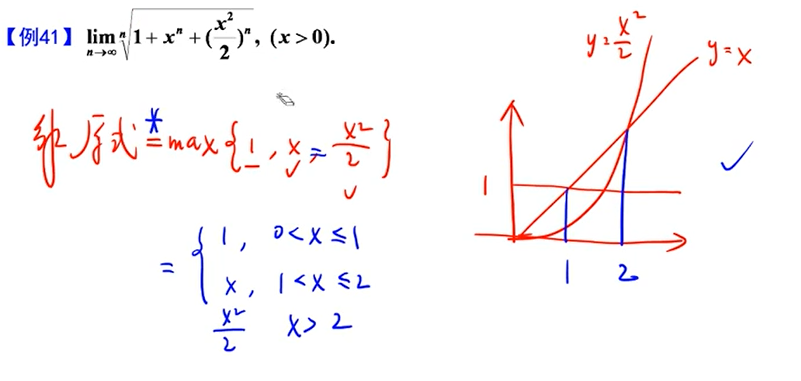
单调有界准则

须先证明极限存在

分子有理化
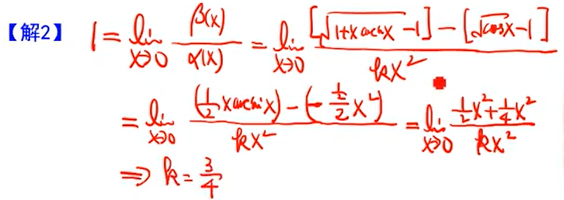 :::tip
:::tip
(1+x)^α^-1 ~ αx== ==1-cos^α^x ~ (α/2)x^2^
:::



————强化题型












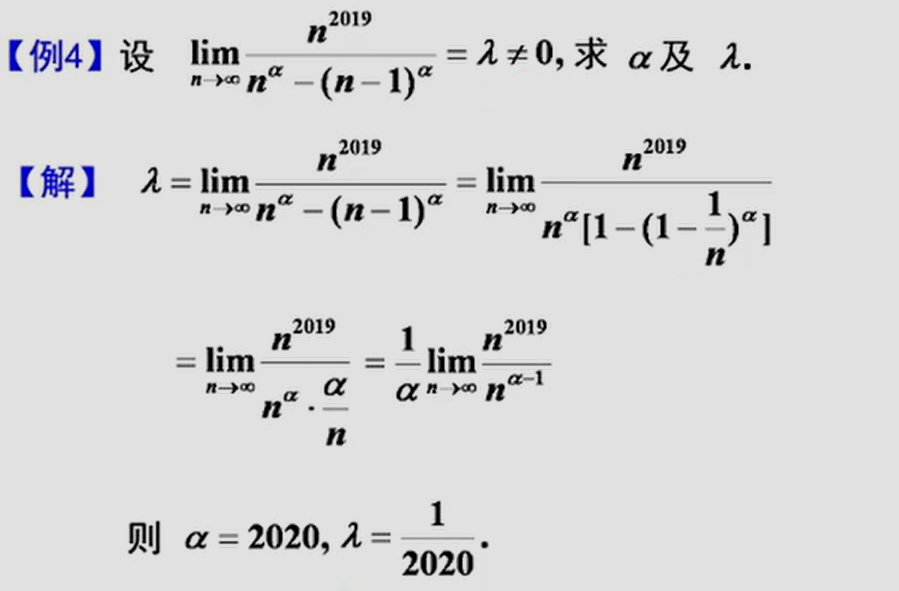



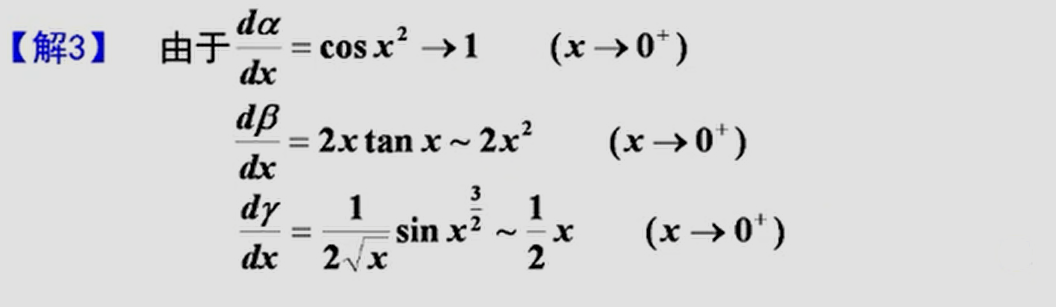
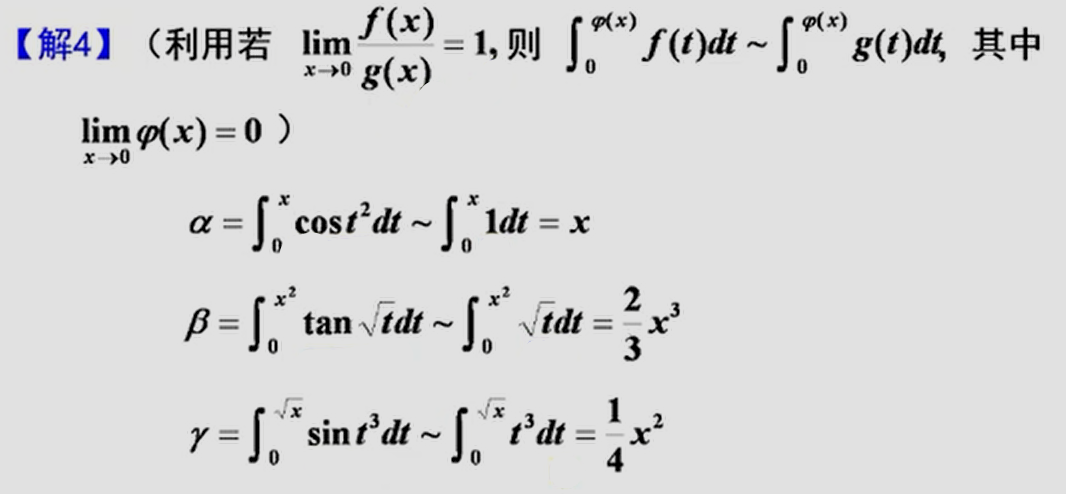

三、连续
1、连续的概念
定义4: 区间上的连续。(a,b)连续即区间内所有点连续,不包含端点;[a,b]连续即要求端点a右连续,端点b左连续。
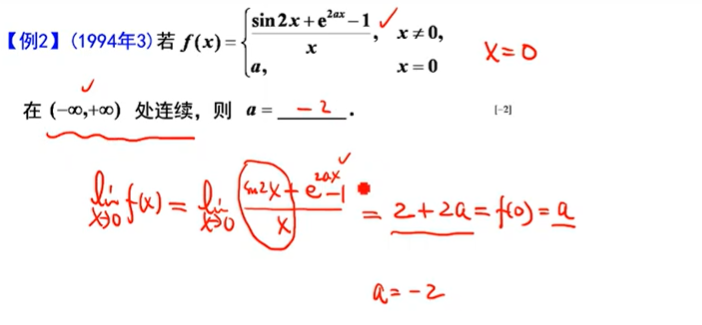
2、间断点及其分类
**定义:**若f(x)在某去心领域有定义,但在X
0处不连续,则称X0为f(x)的间断点
分类:
判断并说明间断点时第一类必须精确到细分类,第二类不用再细分


选A。x=0和x=1无定义,且x=0有极限则为可去间断点;x=1左右极限不等则为跳跃间断点
3、连续函数的性质


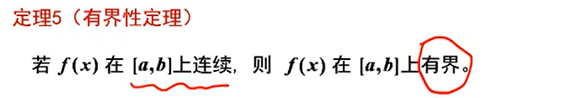

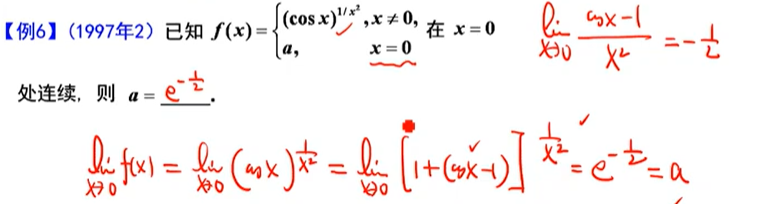
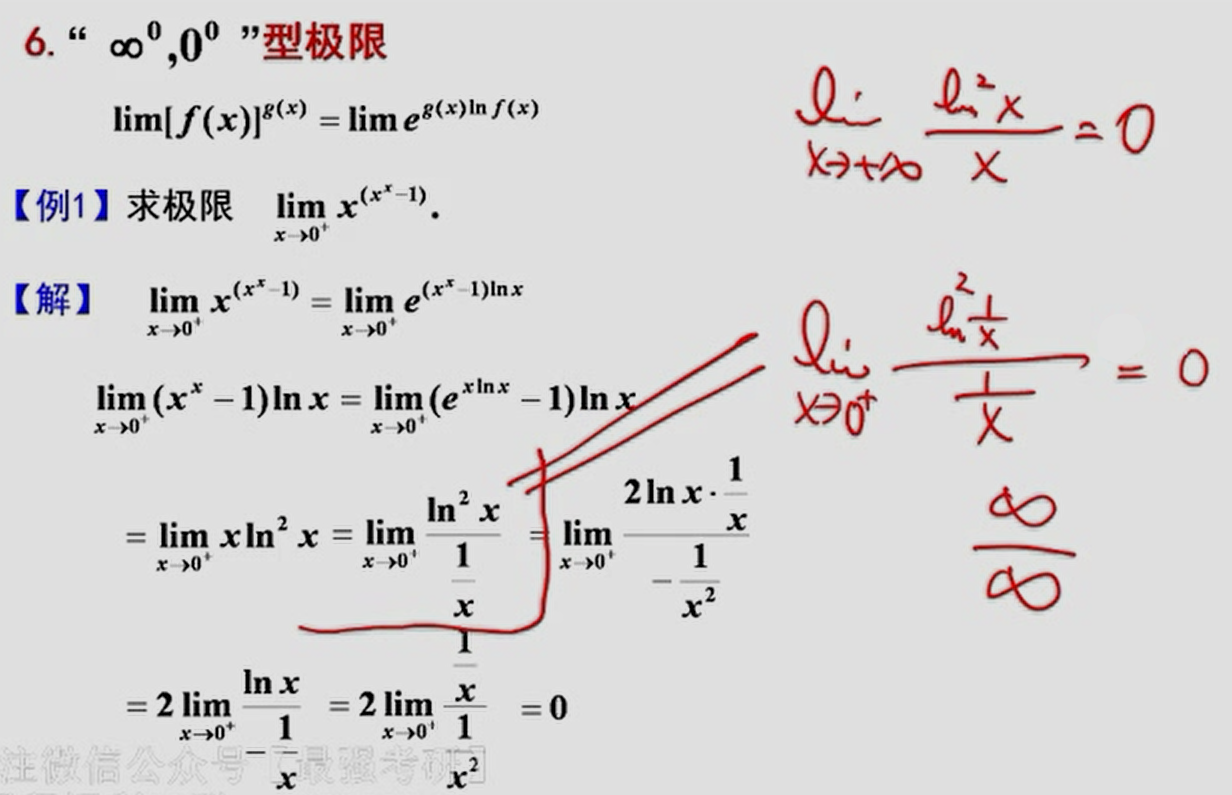
1^∞^型极限

x-->1时需判断左右极限


如果是初等函数,则除间断点外其他处处连续

x=1时,左极限≠有极限≠f(1),所以为跳跃间断点;x=-1时,左极限=有极限=f(-1),所以为连续点
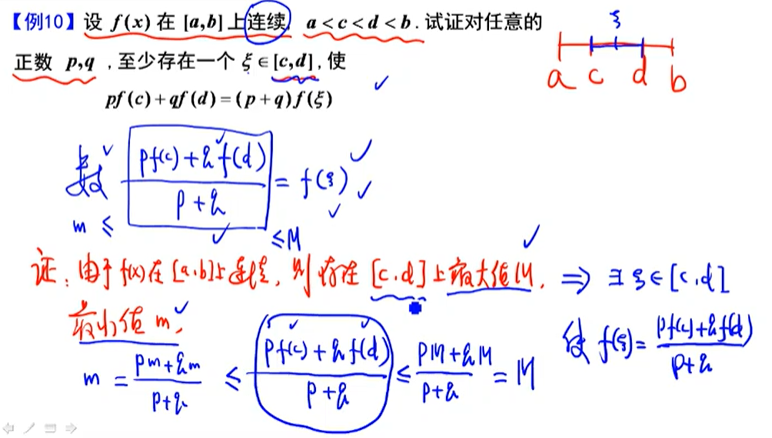
应用最值定理和介值定理。先对式子进行放大缩小
————强化题型





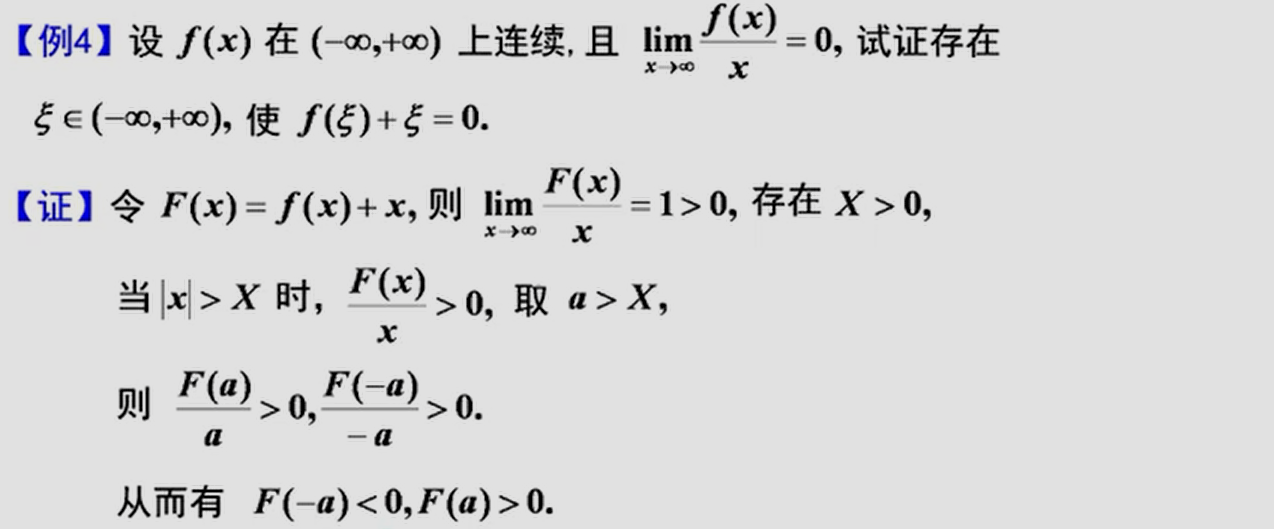
————题型归纳
- 函数性质
- 复合函数
- 极限概念和性质
- 求极限
- 无穷小量阶的比较
- 讨论函数连续性及间断点类型
- 有关闭区间上连续函数性质的证明
导数 微分
一、导数与微分的概念
1、导数的概念
(该点变化率)


x=1处的右极限不能直接带入,因为x取不到1

2、微分概念
(函数改变量的近似值)

3、导数与微分的几何意义
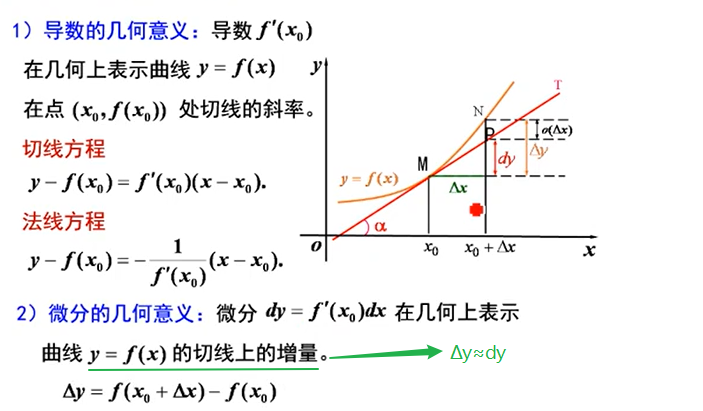
4、连续、可导、可微之间的关系
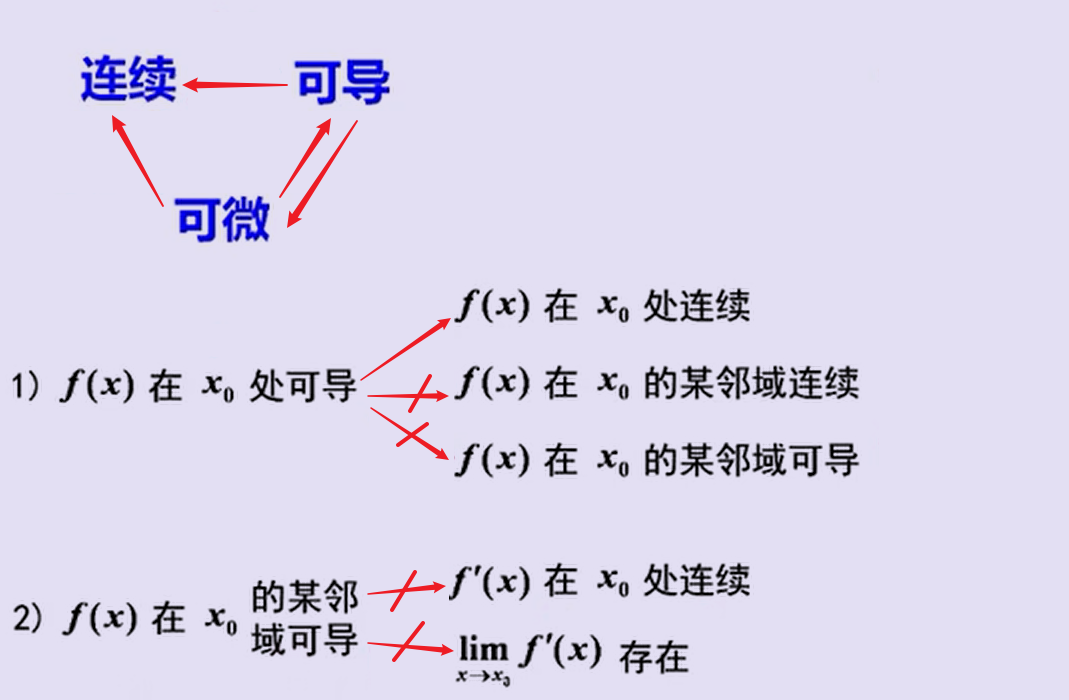

若f(x) n阶可导,则洛必达法则最多能用到(n-1)阶
若f(x) n阶连续可导,则洛必达法则最多能用到 n 阶

二、导数公式及求导法则
1、基本初等函数的导数公式
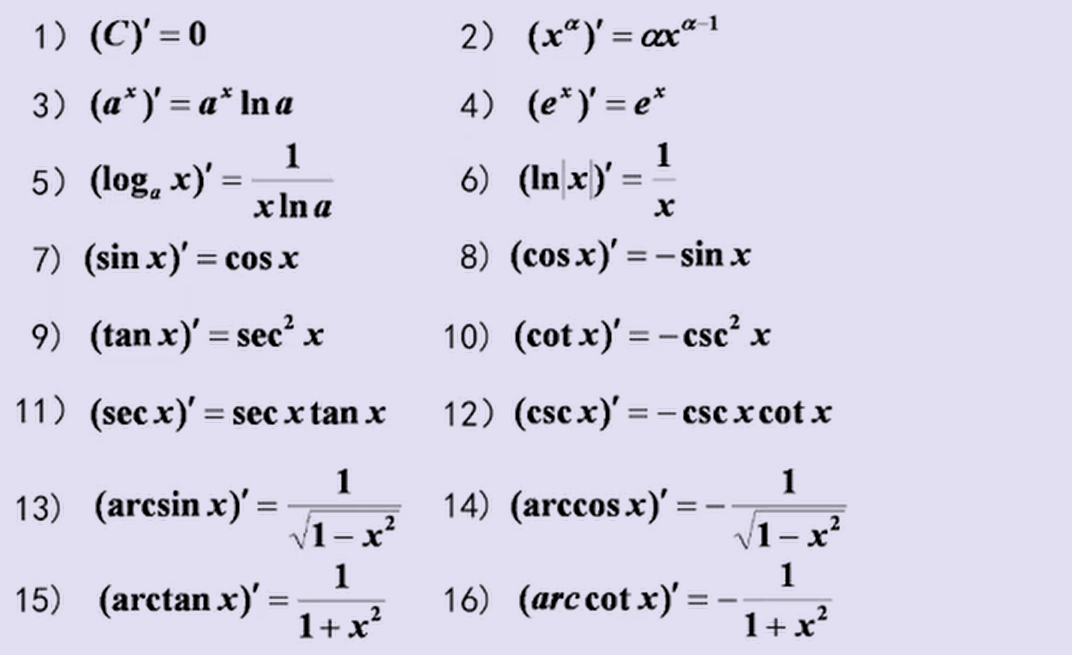
2、求导法则






还可推出φ''(y)=-f''(x)/f '^3^(x)


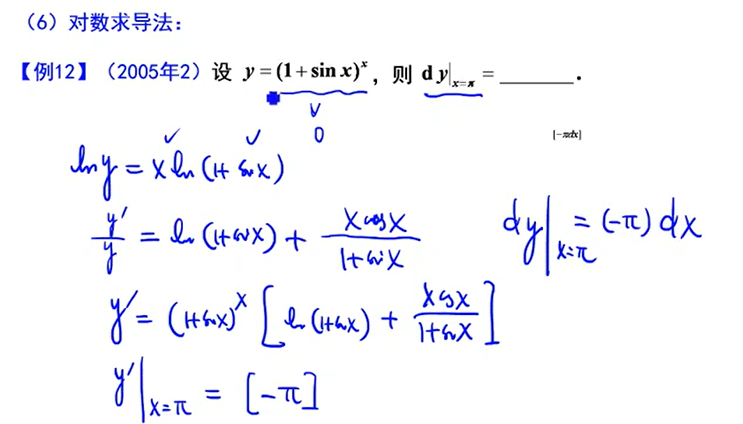
两边同时取对数

三、高阶导数
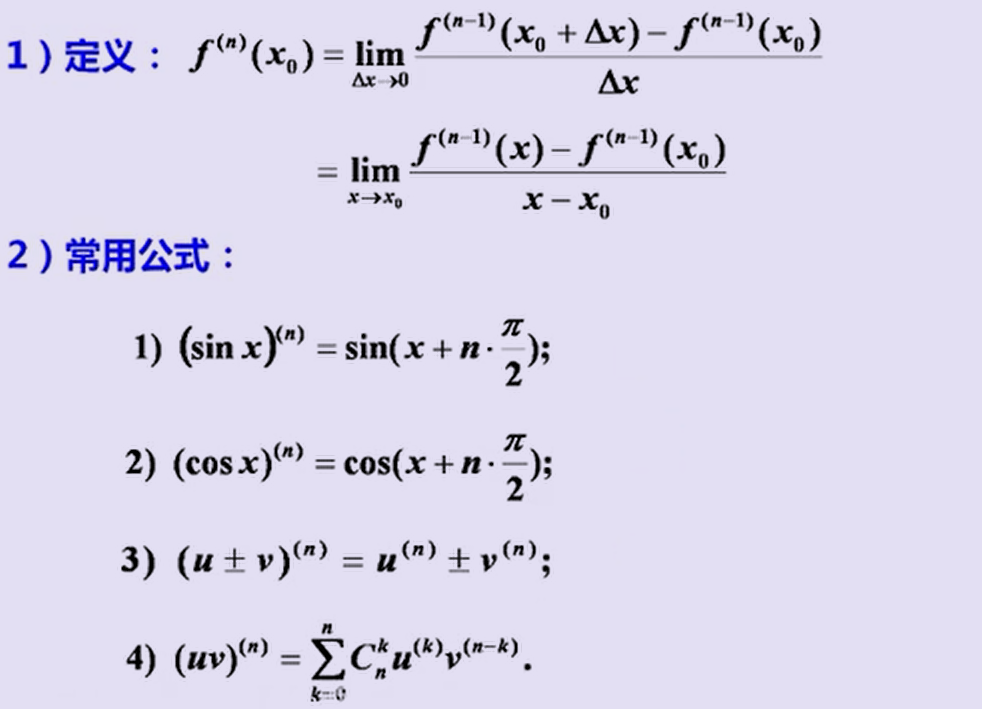
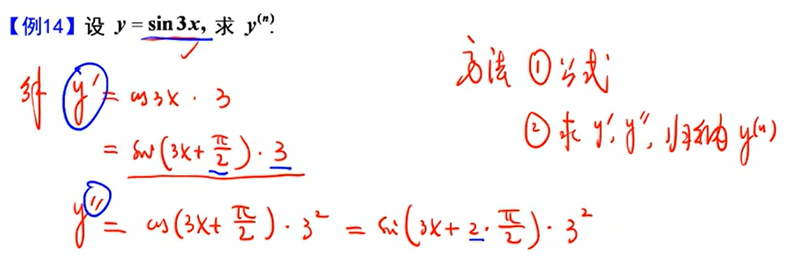
y=sin(ax+b),则y^(n)^=sin(ax+b+nπ/2)×a^n^
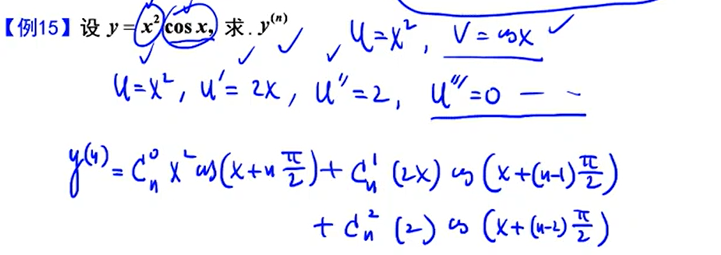
可用莱布尼茨公式

解法二为举特例


f(0)=1,利用导数定义可知要求所给极限,即要求f'(0)

考查导数的定义

A选项只能证明右导数存在;B选项的n默认为正整数;C选项整体极限存在,不能证明单个极限存在


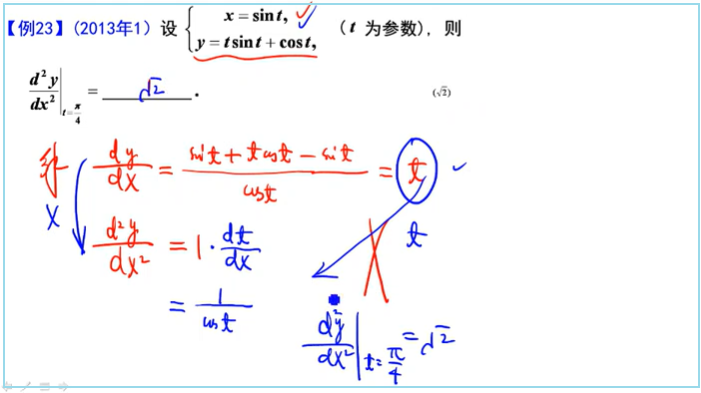


四、导数应用
1、导数的几何意义


2、相关变化率

————强化题型


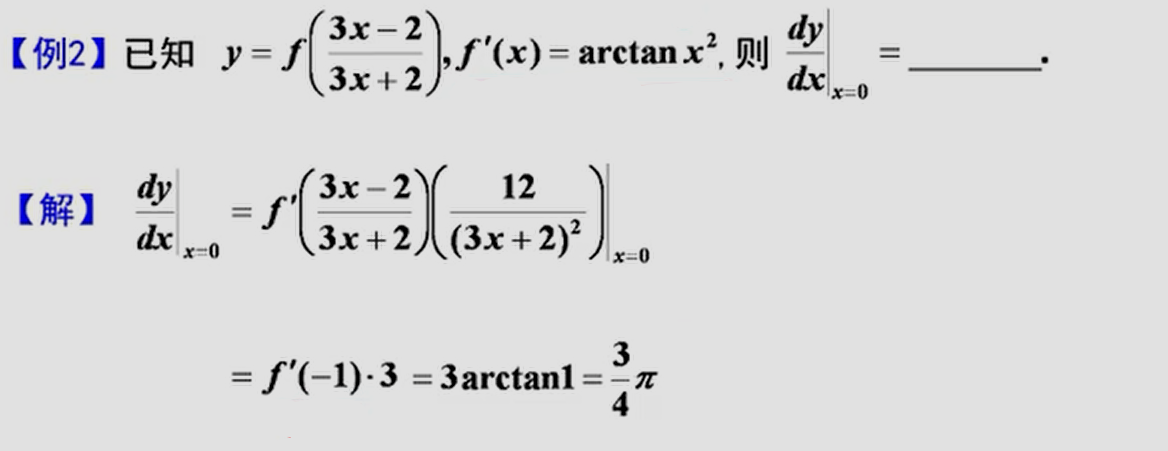



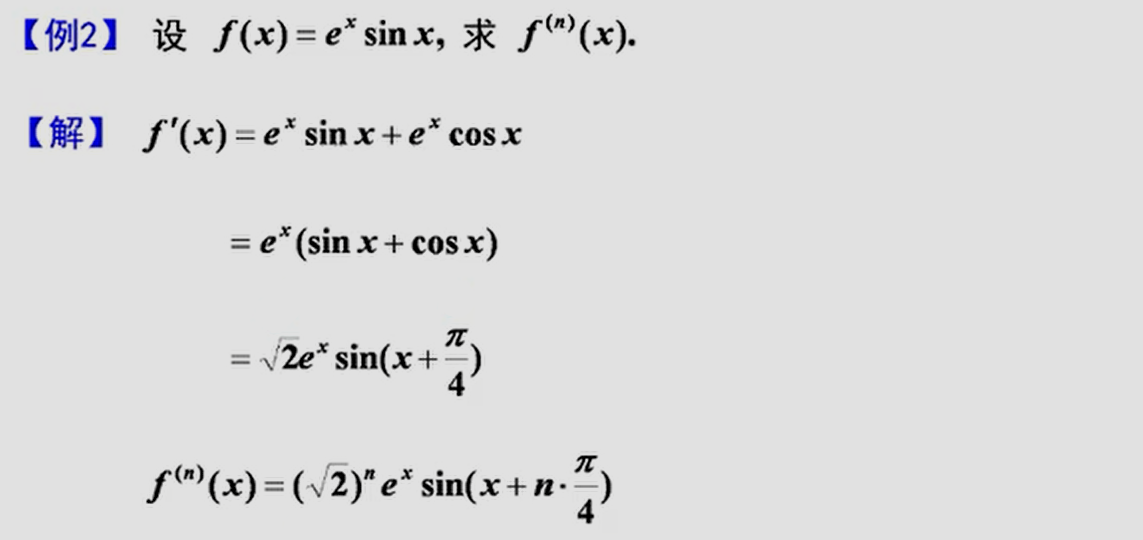
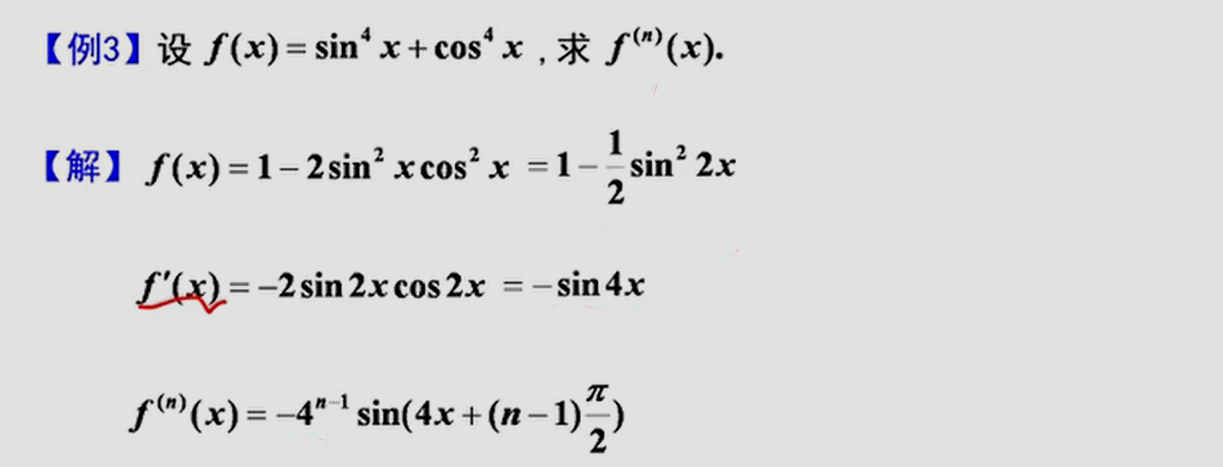
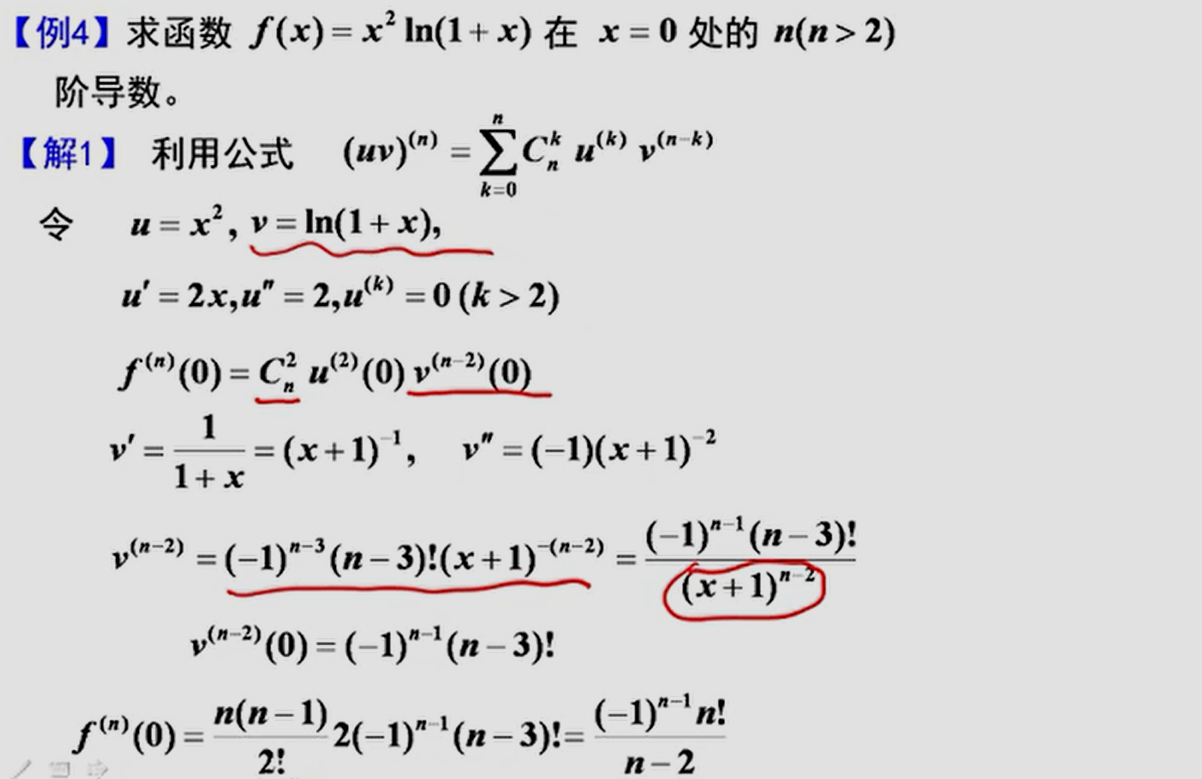
————题型归纳
- 导数定义
- 复合函数、隐函数、参数方程求导
- 高阶导数
- 导数应用
微分中值定理及导数应用
一、微分中值定理
1、罗尔 拉格朗日 柯西

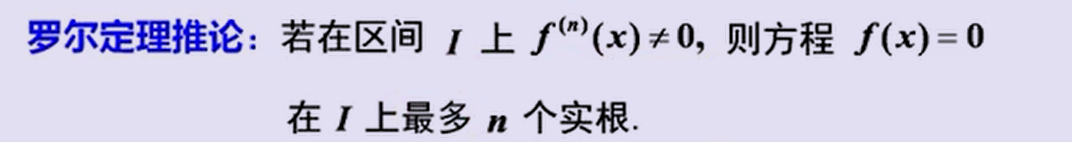


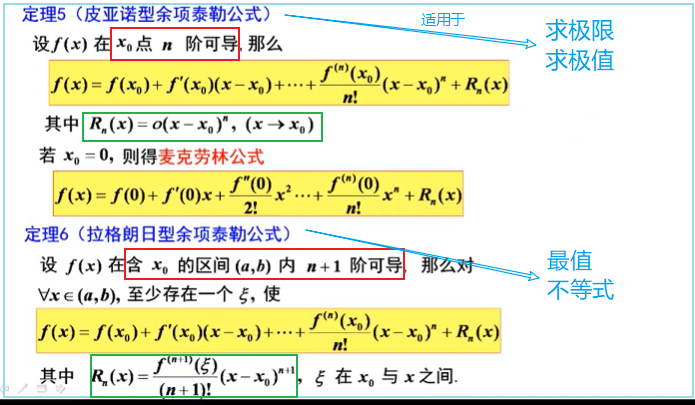
2、常用泰勒公式

二、导数应用
1、函数的单调性

2、函数的极值

极值的必要条件:
若f(x)在X0处可导,且在X0处取得极值,则f '(X0)=0
驻点与极值点的关系:
:::tip
若f(x)可导:那么极值点一定是驻点;驻点不一定是极值点
:::
极值的第一充分条件:

极值的第二充分条件:

3、函数的最大值最小值

若连续函数f(x)在(a,b)内仅有唯一极值点,那么就是最值点
4、曲线的凹凸性
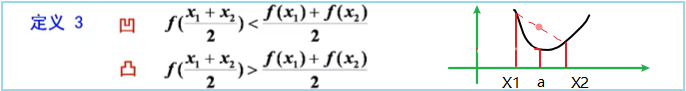

拐点的第一充分条件:
f''(X0)=0,f''(X0)在X0两侧变号,则(X0,f(X0))为拐点
拐点的第二充分条件:
f''(X0)=0,f'''(X0)≠0,则(X0,f(X0))为拐点
5、曲线的渐近线

6、函数的作图
7、函数的弧微分与曲率



相关例题:
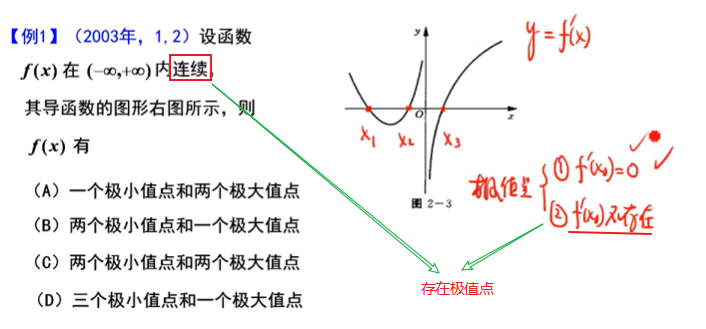
需要注意的是导数不存在的点,如果没有连续这个条件则不一定有极值点
————题型归纳
- 函数极值和最值、曲线的凹向与拐点
- 函数的极值和最值、曲线的凹向与拐点
- 求曲线的渐近线
- 方程的根
- 不等式的证明
- 有关中值定理的证明
————典型例题

用到了极限的保号性
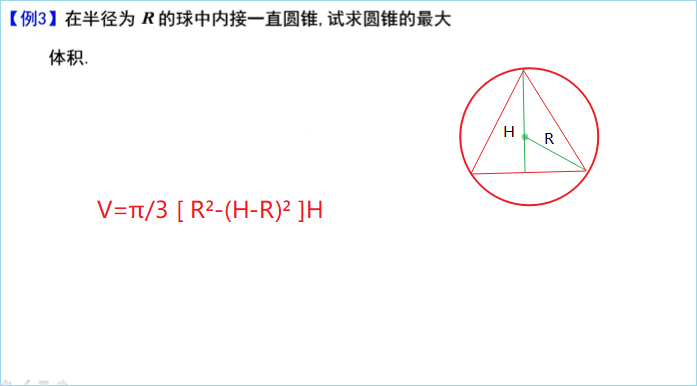




选C。即判断是否有水平、垂直、斜渐近线,解法二:可写成f(x)=ax+b+α(x)就有渐近线
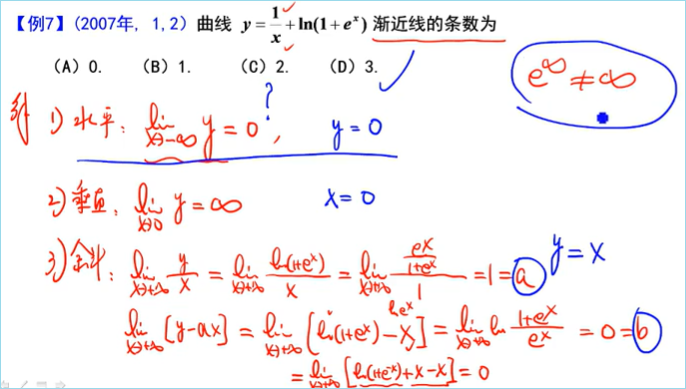
特别注意的是e^∞^≠∞



罗尔定理的应用


拉格朗日的应用





第二问一般解法为构造辅助函数,利用罗尔定理求解
————强化题型





要学会灵活易变





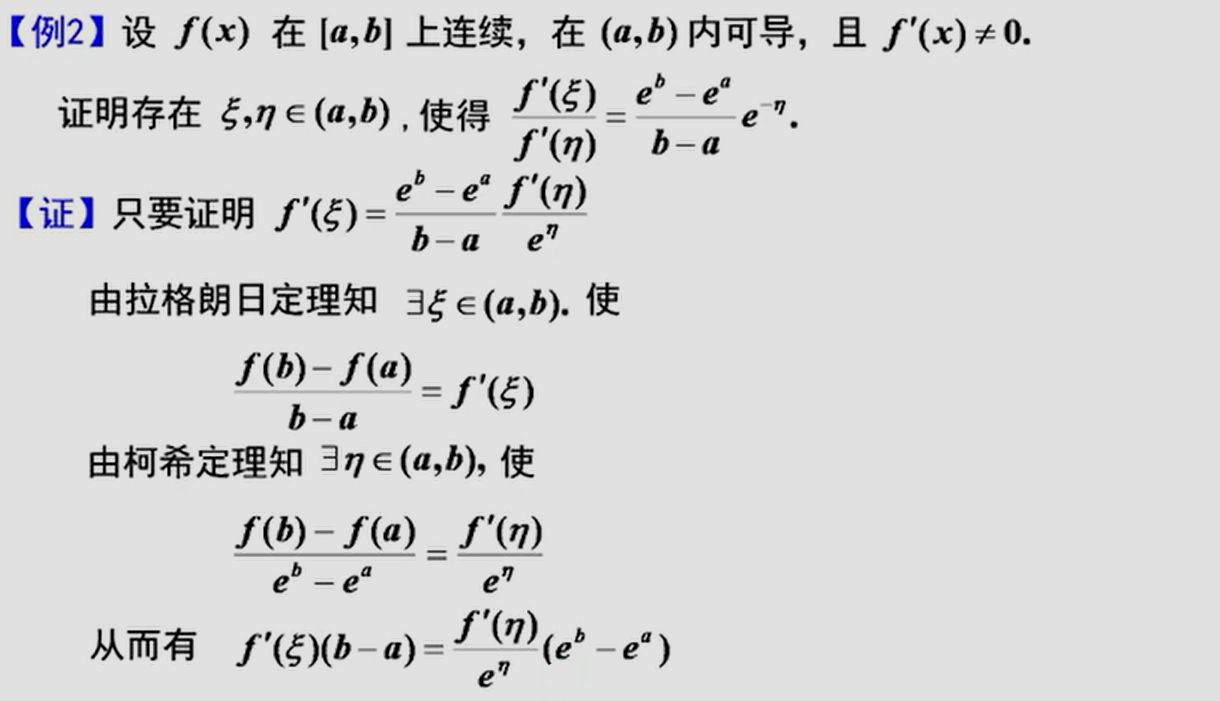




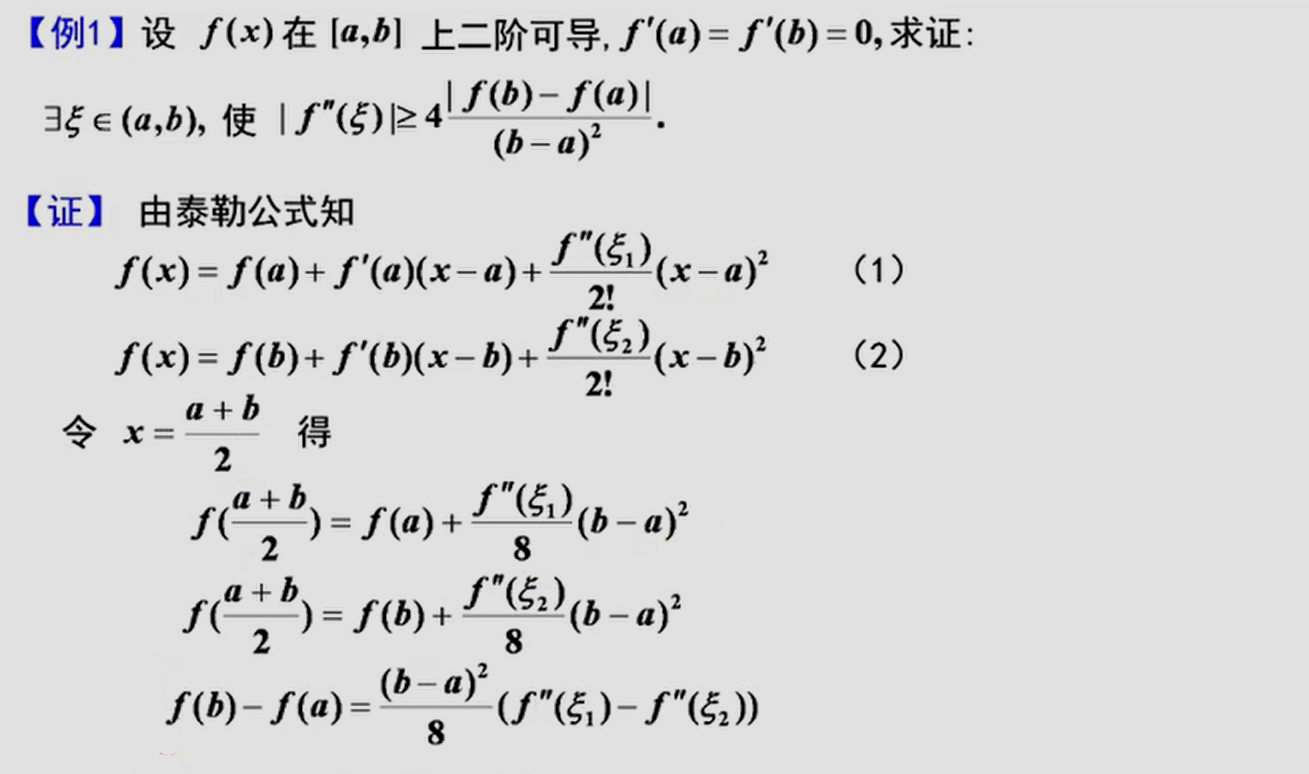


积分学
不定积分
一、概念与性质
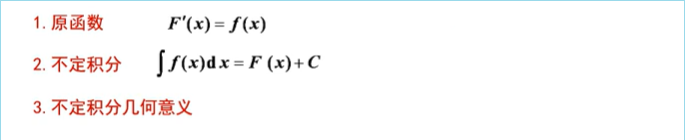



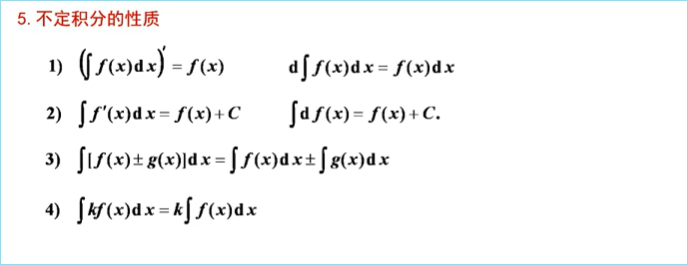
二、不定积分的基本公式
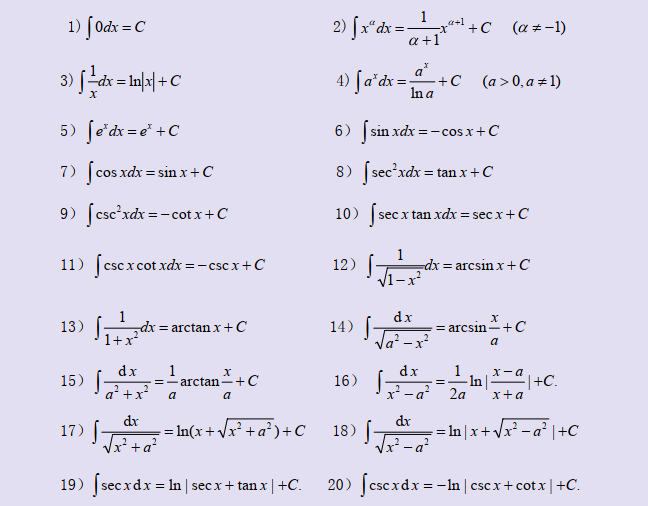

三、三种主要积分法
1、第一类换元法(凑微分法)
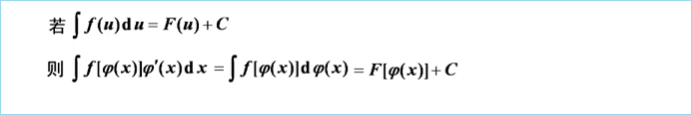

不定积分的解法不同,结果也可能会不同
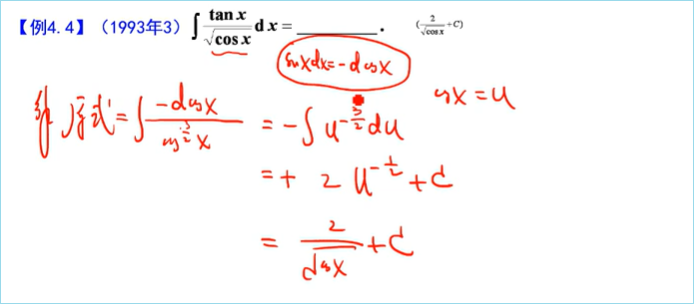


2、第二类换元法




3、分部积分法


四、三类常见可积函数积分
1、有理函数积分
$\int$ R(x) dx
(1)一般法(部分分式法)
(2)特殊方法(加项减项拆或凑微分降幂)
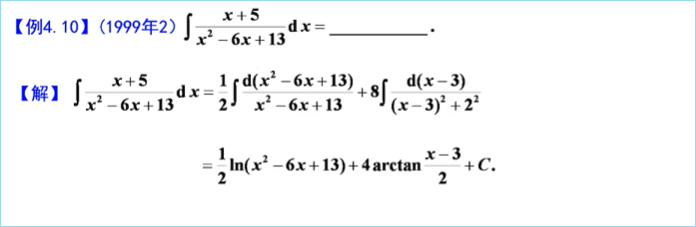
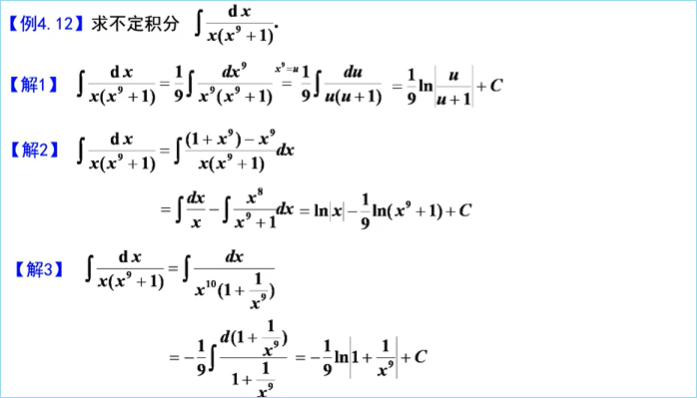
2、三角有理式积分




3、简单无理函数积分
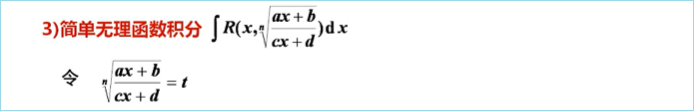

————题型归纳
- 求积分(换元、分部)
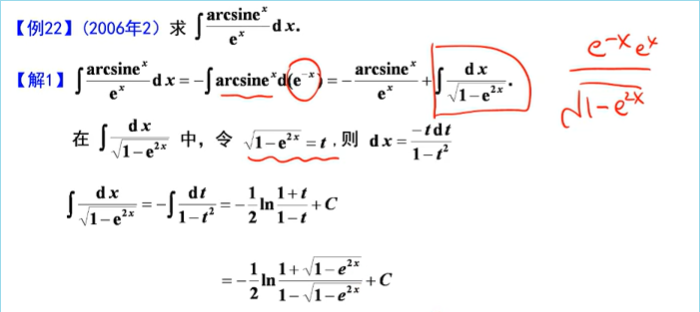
————典型例题

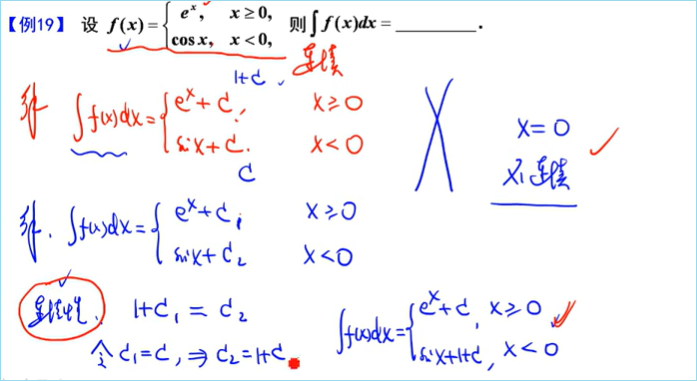
需要讨论连续性


解法二为排除法

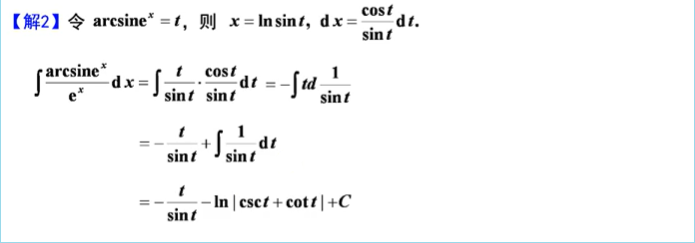




定积分
一、定积分的概念和几何意义


二、定积分的性质

f(x)为奇函数,则$\int_{0}^{x}{f(t)}dt$ 为偶函数;
f(x)为偶函数,则$\int_{0}^{x}{f(t)}dt$ 为奇函数;
证明如下:
设 F(x) = $\int_{0}^{x}{f(t)}dt$ $$ F(-x)=\int_{0}^{-x}{f(t)}dt=\int_{0}^{x}-{f(u)}d(-u)=\int_{0}^{x}{f(u)}du=\int_{0}^{x}{f(t)}dt=F(x) $$
三、积分上限的函数
$$ \int_{a}^{x}{f(t)}dt $$

四、定积分的计算
牛顿-莱布尼茨公式: $$ \int_{a}^{b}{f(x)}dx=F(b)-F(a) $$
换元法: $$ \int_{a}^{b}{f(x)}dx=\int_{α}^{β}{f(φ(t))φ'(t)}dt $$
分部积分法: $$ \int_{a}^{b}{u}dv=uv|{a}^{b} -\int{a}^{b}{v}du $$
利用奇偶性、周期性:

点火公式:
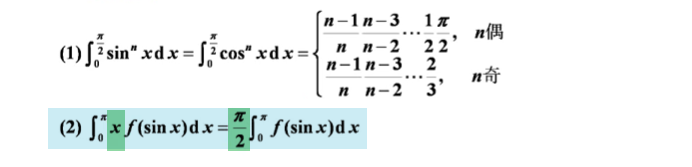
————题型归纳
- 定积分的概念、性质及几何意义
- 定积分计算
- 变上限定积分
————典型例题
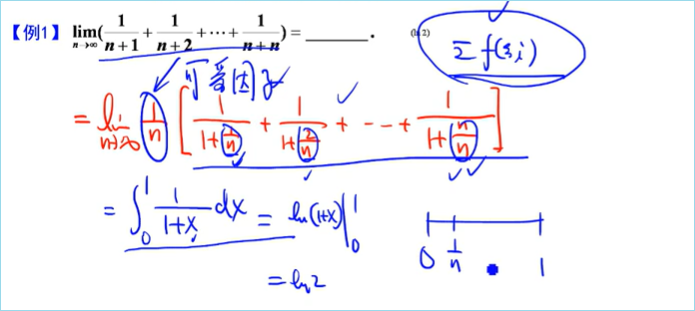
提可爱因子
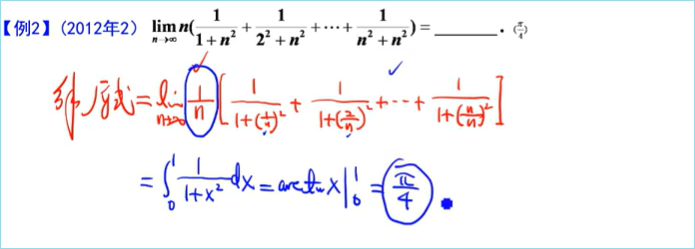
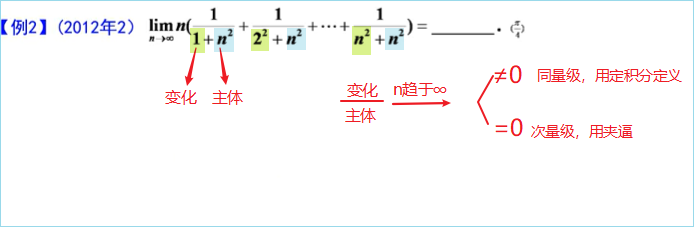
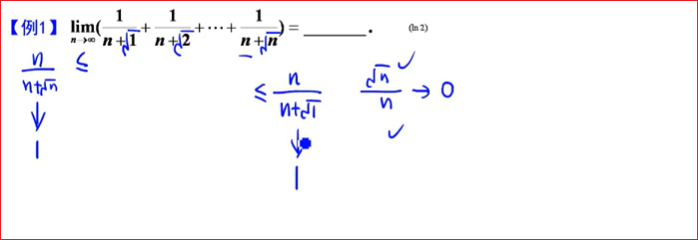
此题就用夹逼原理
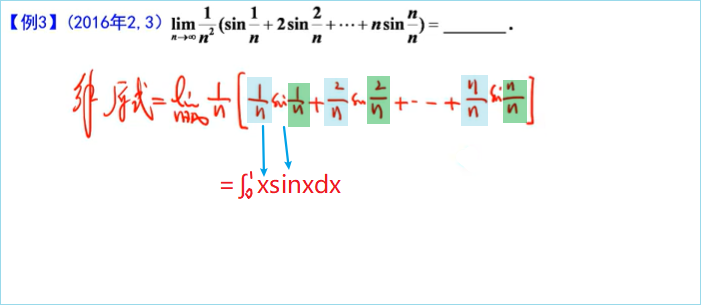
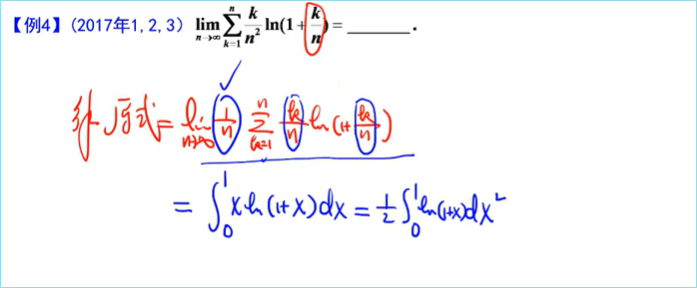

需要注意在使用定积分的几何意义时必须满足积分上限大于积分下限
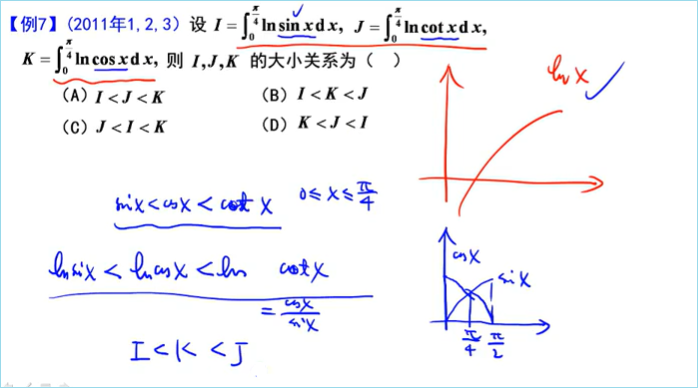


积分中值定理以及罗尔定理的应用

①熟记sin^n^x积分公式;②判断奇偶

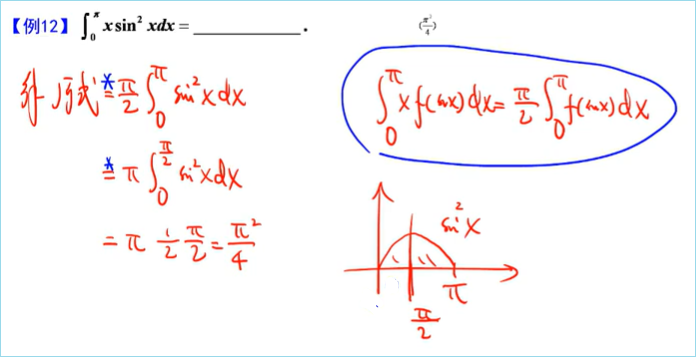
巧用公式





变上限定积分:
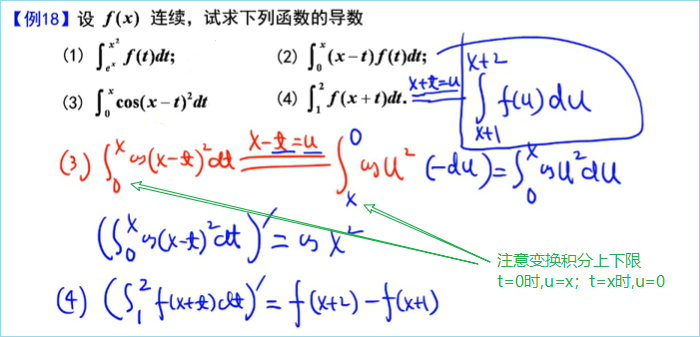








隐函数求导
反常积分
一、相关定义

————题型归纳
- 反常积分的敛散性
- 反常积分的计算
————典型例题



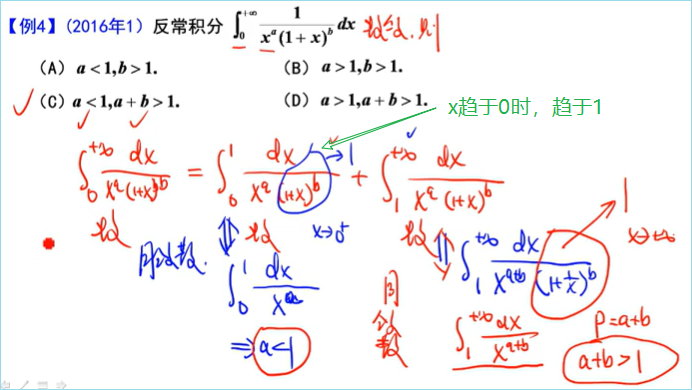
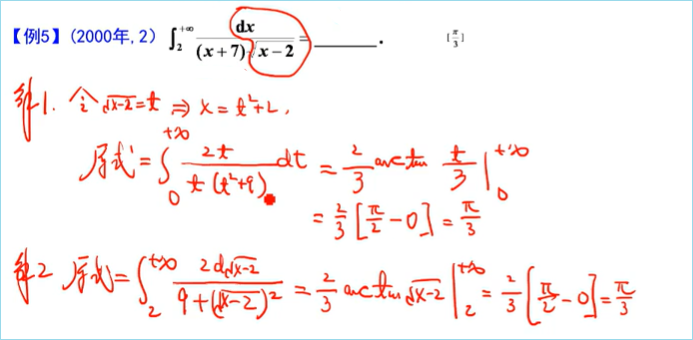
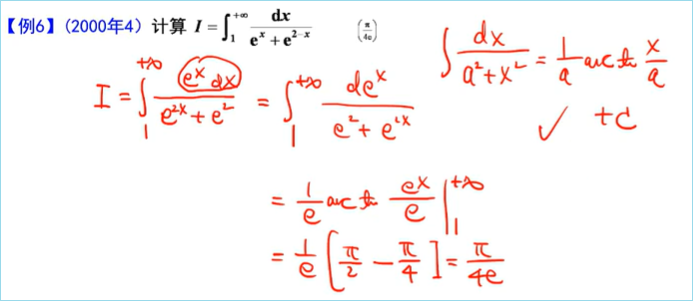
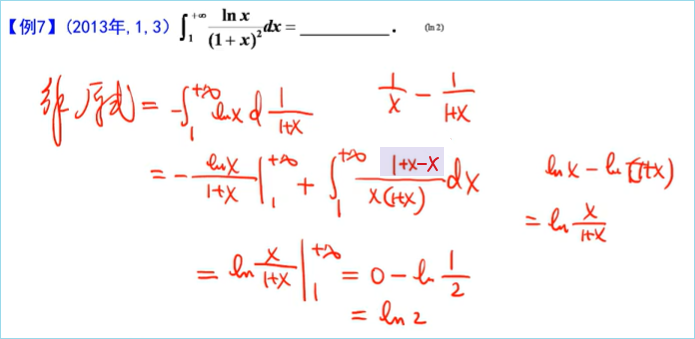
定积分的应用
一、几何应用
1、平面图形的面积

2、旋转体体积

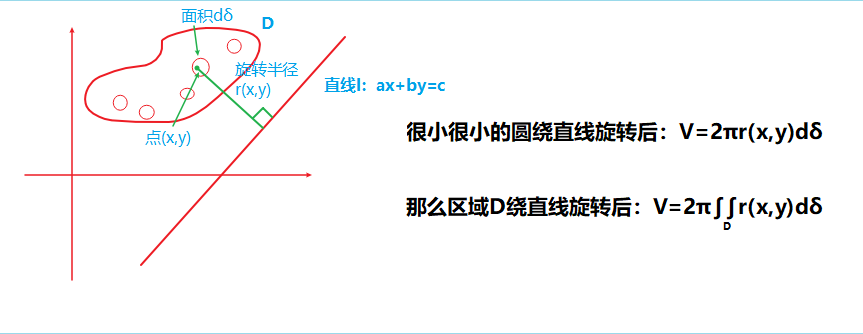

3、曲线弧长
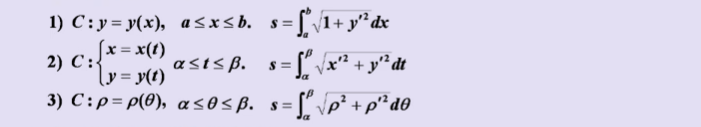
4、旋转体侧面积
二、物理应用

求面积可转换为二重积分




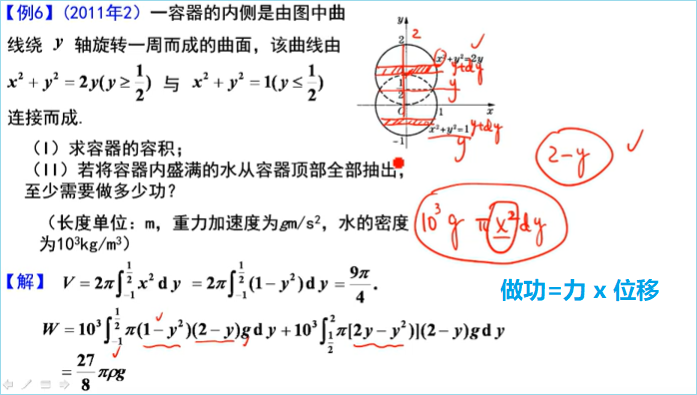
建立微元思想
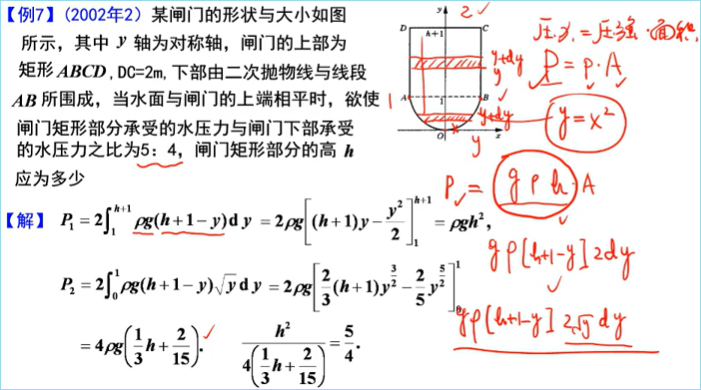
微分方程
一、微分方程的基本概念
-
微分方程:含有未知函数的导数或微分的方程
-
微分方程的阶:方程中所含未知函数的导数的最高阶数
-
微分方程的解:y=φ(x)带入y‘能成为恒等式,则y=φ(x)称为它的解
-
微分方程的通解:方程的解中含有任意常数C,且独立任意常数个数和方程的阶数相同
-
微分方程的特解:得出了任意常数C的解
-
初始条件:确定特解的一组常数称为初始条件
-
积分曲线:微分方程的解所对应的曲线
二、一阶微分方程
1、可分离变量的方程 y' = f(x)g(y)

2、齐次方程
$$ \frac{dy}{dx}=φ(\frac{y}{x}) $$

3、线性方程
$$ y'+P(x)y=Q(x) $$

4、伯努利方程
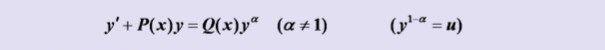
5、全微分方程

三、可降阶方程
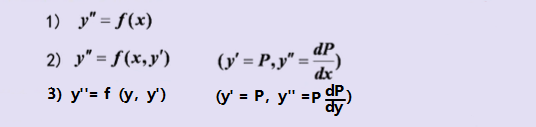


x=0时y=1,y'=1/2,则C=1/2
四、高阶线性微分方程
1、线性微分方程的解的结构

两者之比不为常数,则线性无关

2、常系数齐次线性微分方程
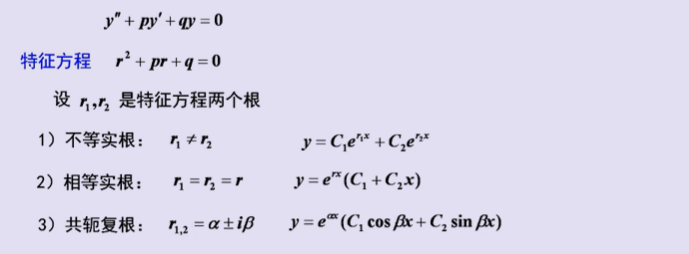



3、常系数非齐次线性微分方程
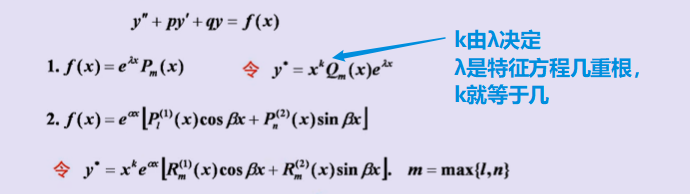
其中Qm(x) 是与Pm(x) 同次的多项式
其中Pl(1) (x) ,Pn(2) (x) 分别为x的l 次,n次多项式;Rm(1) (x) ,Rm(2) (x) 是两个m次多项式


将特解代入原方程可求得a
4、欧拉方程
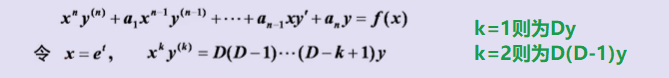
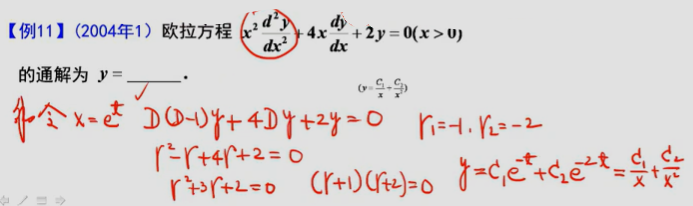
5、差分方程(:::tip
仅数三
:::)

————题型归纳
- 微分方程求解
- 综合题
- 应用题
————典型例题

lnx-lny=ln(x/y),从而转换为齐次方程结构
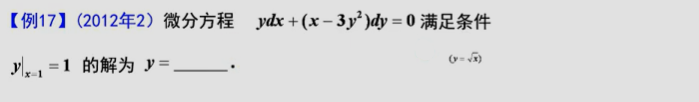

线性方程



将e^2x^代入非齐次方程左右式子不可能相等,则e^2x^是齐次解,若xe^x^也是齐次解,其λ=1,满足的是相等实根的解的表达式,但此方程是二阶方程,特征方程最多两个根,若1是二重根,加上之前的e^2x^就是3个根,矛盾,所以xe ^x^只能是非齐次解










多元函数微积分
微分学
重极限 连续 偏导数 全微分
一、二元函数的极限
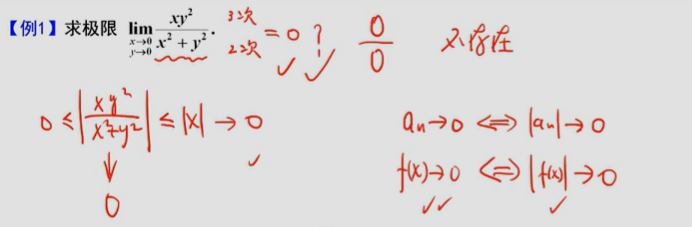
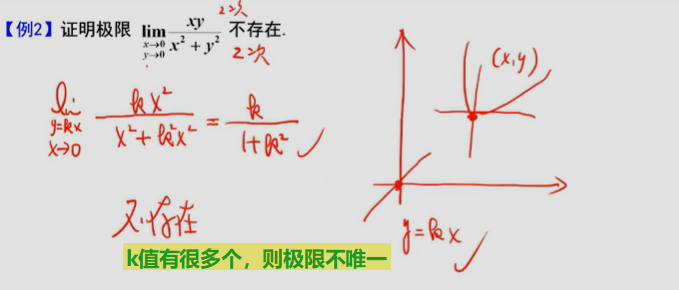
二、多元函数的连续性
1、连续的概念
$$ \lim_{(x,y)\rightarrow(x_o,y_0)}f(x,y)=f(x_0,y_0) $$
2、连续函数的性质
- 多元函数的和、差、积、商(分母不为0)仍为连续函数
- 多元函数的复合函数也是连续函数
- 多元函数在其定义区域内连续
- (最大值定理)有界闭区域D上的连续函数在区域D上必能取得最大值与最小值
- (介值定理)有界闭区域D上的连续函数在区域D上必能取得介于最大值与最小值之间的任何值
三、偏导数
1、偏导数的定义
$$ f_x(x_0,y_0)= \lim_{Δx\rightarrow0}\frac{f(x_0+Δx,y_0)-f(x_0,y_0)}{Δx}=\frac{d}{dx}f(x,y_0)|_{x=x_0} $$
$$ f_y(x_0,y_0)= \lim_{Δy\rightarrow0}\frac{f(x_0,y_0+Δy)-f(x_0,y_0)}{Δy}=\frac{d}{dy}f(x_0,y)|_{y=y_0} $$
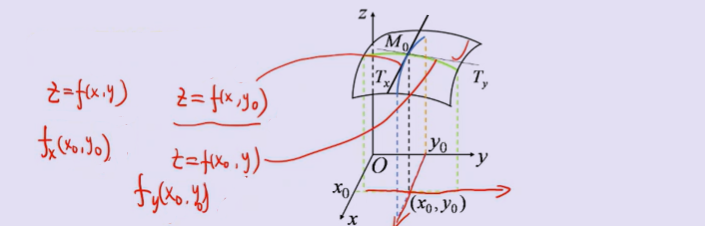
2、二元函数偏导数的几何意义
fx′(x0 , y0 ) 表示上述交线在点M 处的切线对x 轴的斜率
fy′(x0 , y0 ) 表示��上述交线在点M 处的切线对 y 轴的斜率
3、高阶偏导数

4、全微分


5、连续、可偏导及可微之间的关系
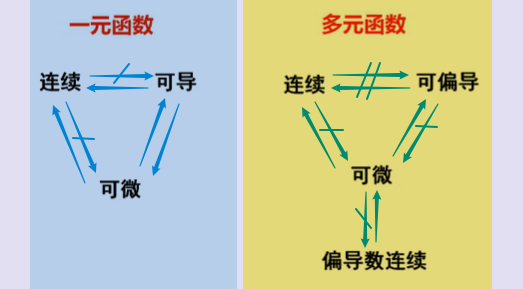
————题型归纳
讨论连续性、偏导数、全微分的概念及其之间的关系
————典型例题


投机取巧法:取f(x)=2x-y+2,则df=2dx-dy,好神奇哈哈哈


多元函数微分法
一��、复合函数的微分法
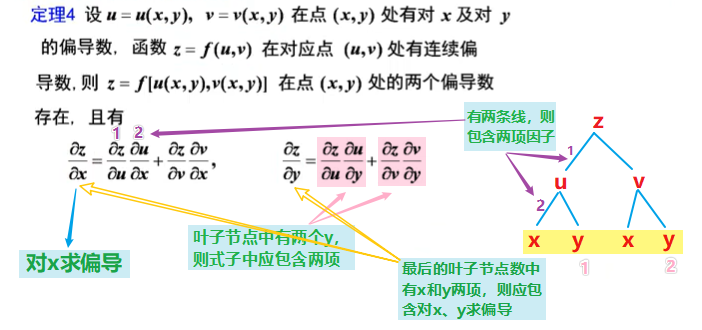
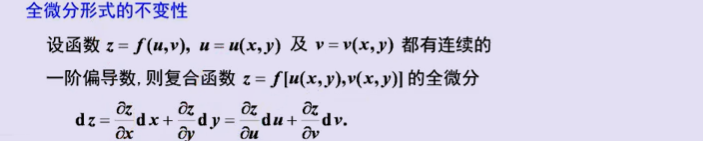
二、隐函数的微分法

————题型归纳
- 复合函数的偏导数与全微分的计算
- 隐函数的偏导数与全微分
————典型例题



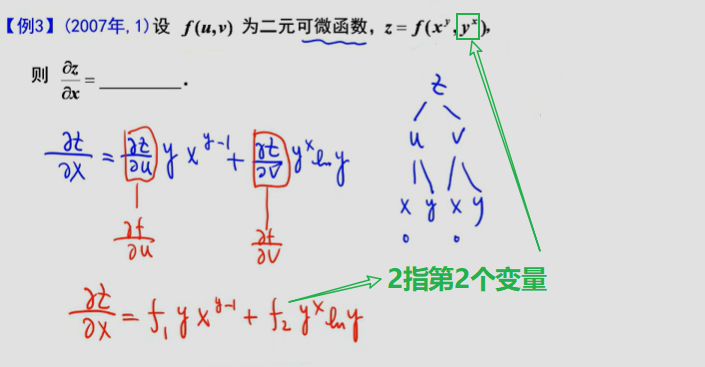

结果为:f₁ (1,1) + f₁₁ (1,1) - f₂ (1,1)

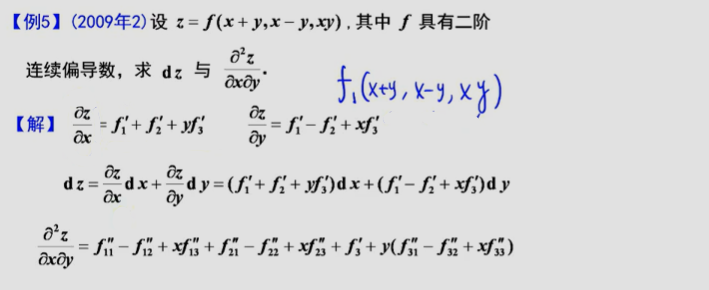


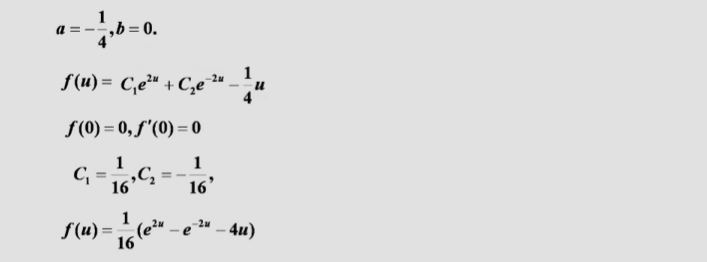



方法2中要把u看做常数
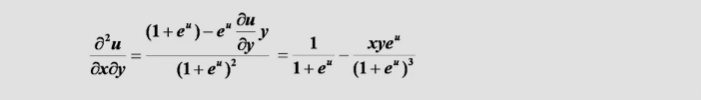





三、多元函数的极值与最值
1、无约束极值


2、条件极值与拉格朗日乘数法

3、最大值与最小值

————题型归纳
- 求极值(无条件)
- 求连续函数 f (x,y) 在有界闭区域D上的最值
- 最值应用题
————典例例题


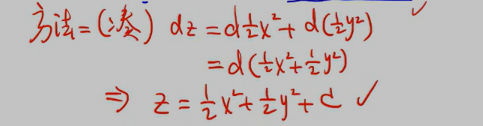






��积分学
向量代数与空间解析几何
一、向量代数
1、数量积

2、向量积

3、混合积


混合积中只要包含两项相同的就=0
二、空间平面与直线
1、平面方程
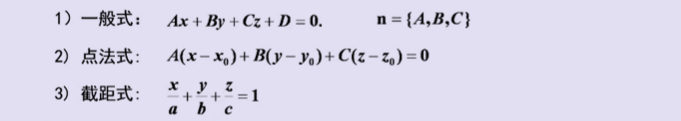
2、直线方程
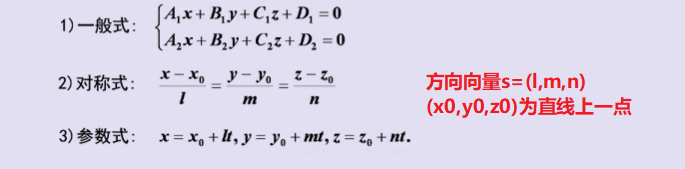
3、平面与直线的位置关系
关键:平面的法线向量,直线的方向向量
4、点到面的距离
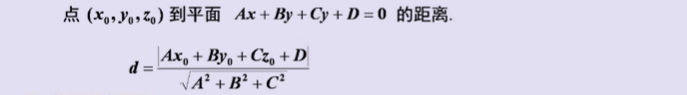
5、点到直线的距离

————典型例题




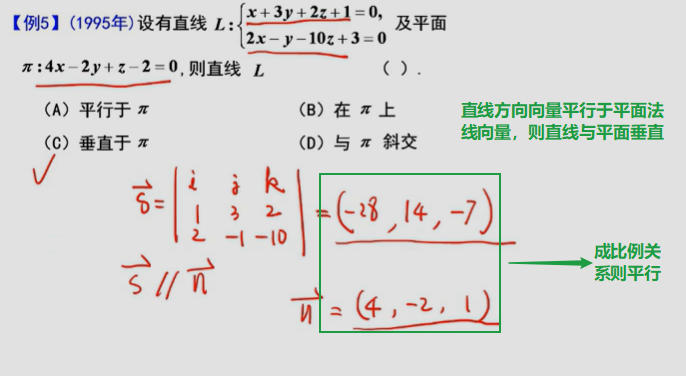
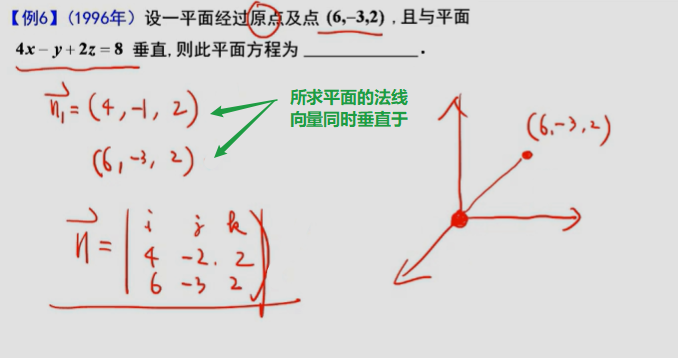

三、曲面与空间曲线
1、曲面方程
2、空间曲线

3、常见曲面



4、空间曲线投影

————典型例题
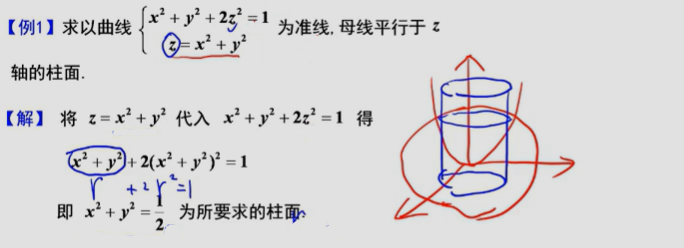

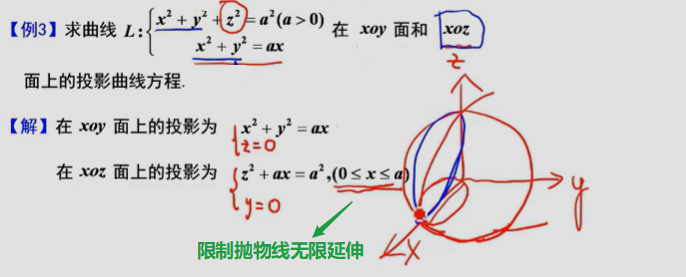
四、多元微分在几何上的应用
1、曲面的切平面与法线
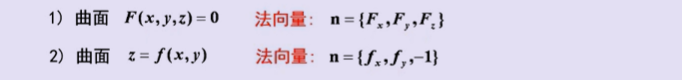
2、曲线的切线与法平面
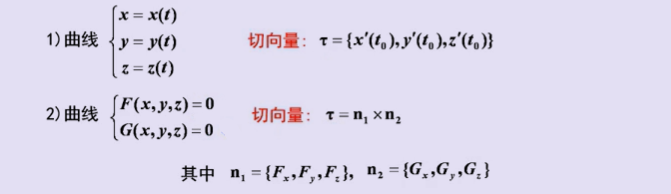
————题型归纳
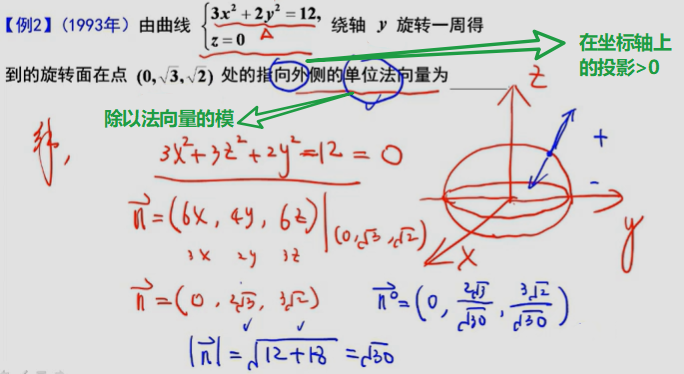
建立曲面的切平面和法线及曲线的切线和法平面
————典型例题




二重积分
一、二重积分的概念及性质
1、二重积分的概念
$$ \iint_{D} f(x,y) d\sigma=\lim_{\lambda\rightarrow0}\sum_{i=1}^n f(x_i,y_i)\Delta\sigma_i $$
几何意义:
曲顶柱体的体积
2、二重积分的性质
不等式性质:
- 在D上若 f(x,y) $\leqslant$ g(x,y),则$\iint_{D} f(x,y) d\sigma \leqslant\iint_{D} g(x,y) d\sigma$
- 在D上有m$\leqslant$f(x,y)$\leqslant$M ,则 mS $\leqslant\iint_{D} f(x,y) d\sigma \leqslant$MS(其中S为区域D的面积)
- $|\iint_{D} f(x,y) d\sigma| \leqslant\iint_{D} |f(x,y)| d\sigma$
中值定理:
$\iint_{D} f(x,y) d\sigma=f(\xi,n)\bullet S $
二、二重积分的计算
1、利用直角坐标计算
![]()
![]()
2、利用极坐标计算

3、利用对称性和奇偶性
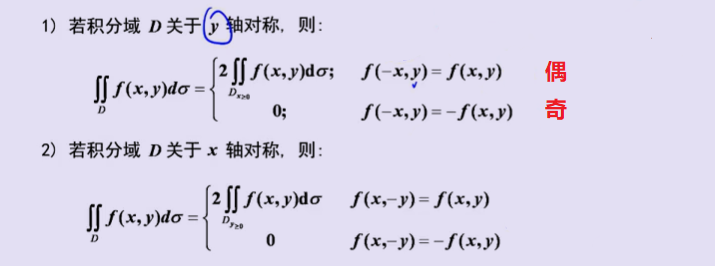
4、利用变量对称性计算
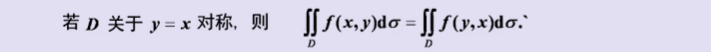
————题型归纳
- 累次积分交换次序或计算
- 二重积分计算
————典型例题

解决此类问题:先画域,然后重新定限








选好积分顺序可使积分简单

对常数1积分即用1乘其面积

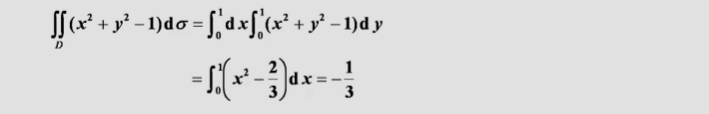


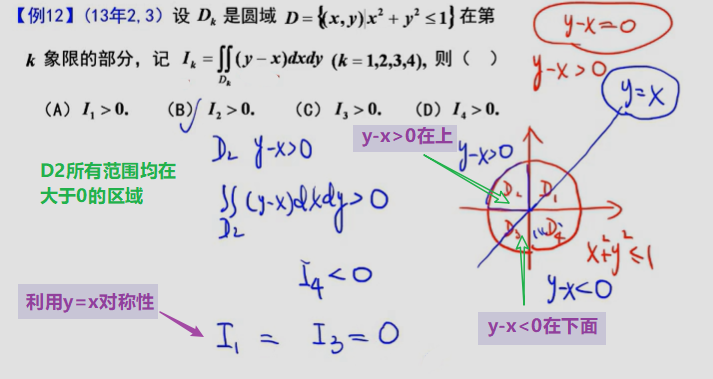
利用了二重积分的不等式性质:被积函数>0,积分就>0

多元积分学及其应用
一、三重积分
1、定义
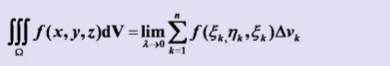
2、性质
3、计算
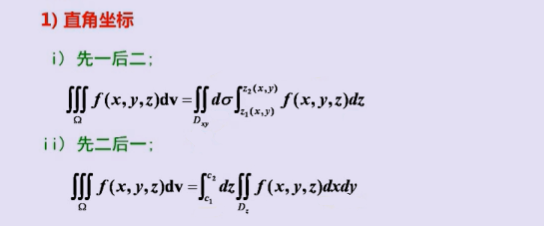
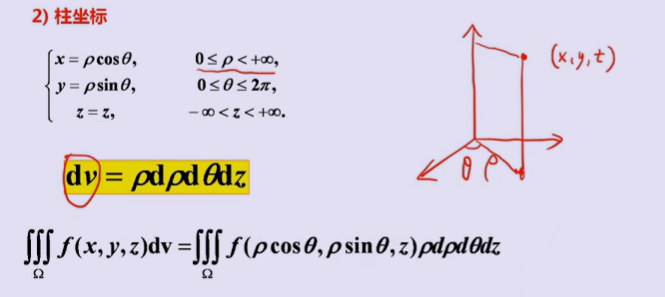
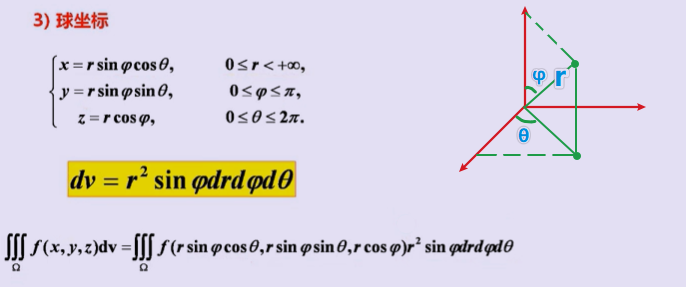


————典型例题


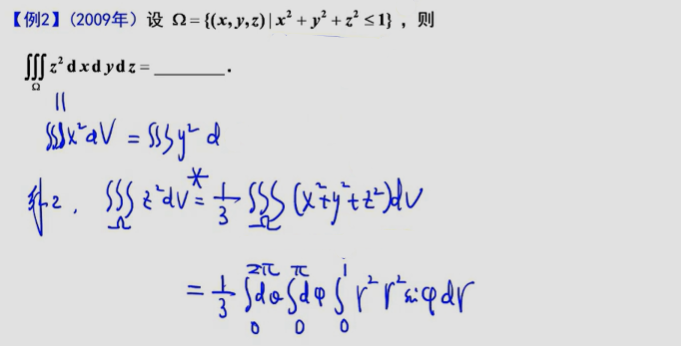
利用变量对称性



此题有多种解法
二、曲线积分
1、对弧长的线积分(第一类)



2、对坐标的线积分(第二类)

第一类线积分要求积分下限小于积分上限,这是第二类与第一类的其中不同之处


单连通:区域内无洞
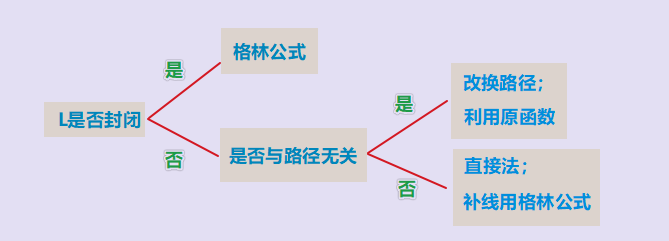
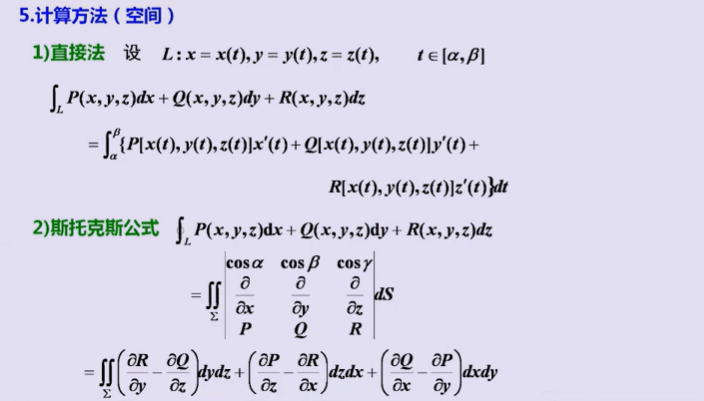
(cosα,cosβ,cosγ)为有向曲面的法向量。方向:四指为路径方向,拇指为法线方向)
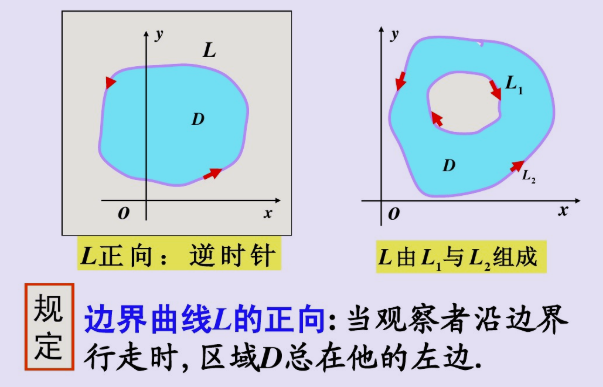
————题型归纳
曲线积分的计算
————典型例题

直接法
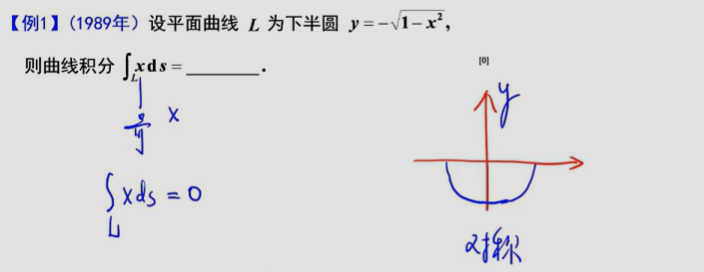
奇偶性
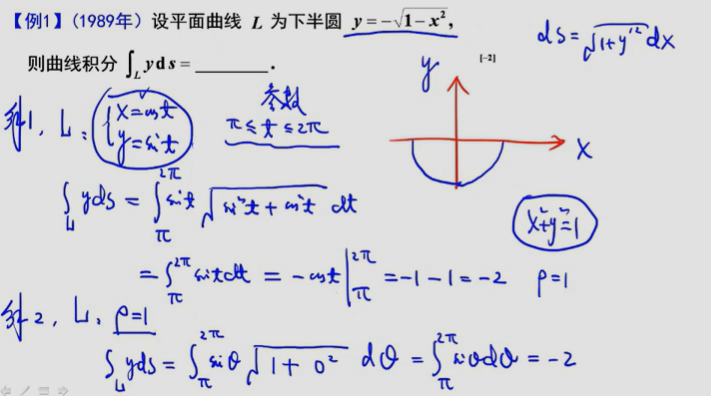
解法1为直接法中的参数方程;解法2为直接法中的极坐标形式
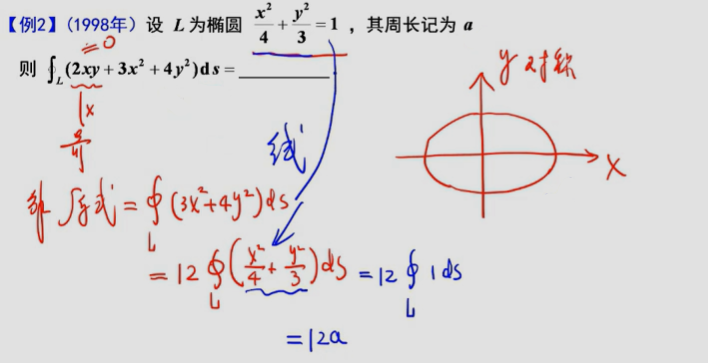


直接法

补线用格林公式

直接法
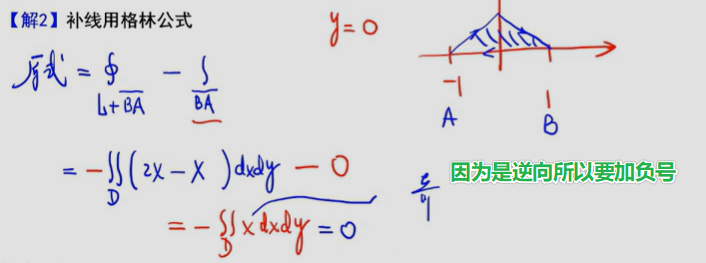
补线用格林公式。注意:使用格林公式前提必须是正向,逆向则要加负号


拆分

直接法

补线用格林公式

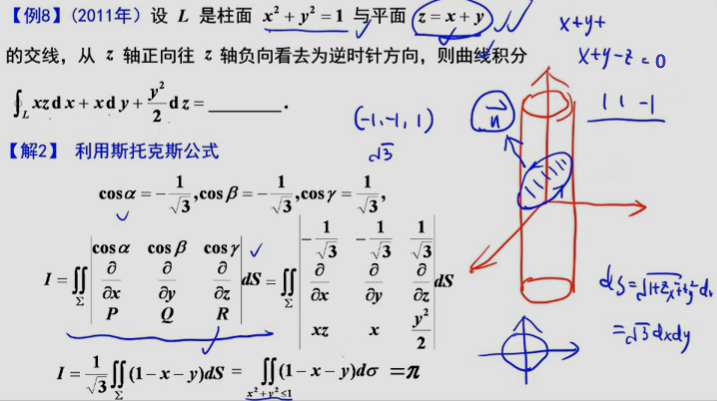
法线向量(1,1,-1)为负向,而应取正向
三、曲面积分
1、对面积的面积分(第一类)

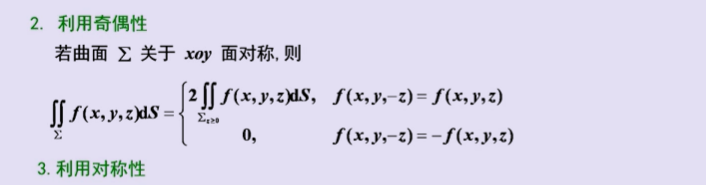
2、对坐标的面积分(第二类)

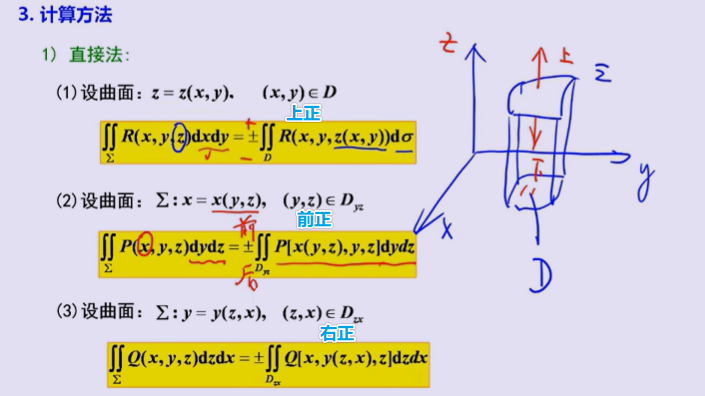


————典型例题

选C




曲面�是封闭的用高斯公式,然后用球坐标计算
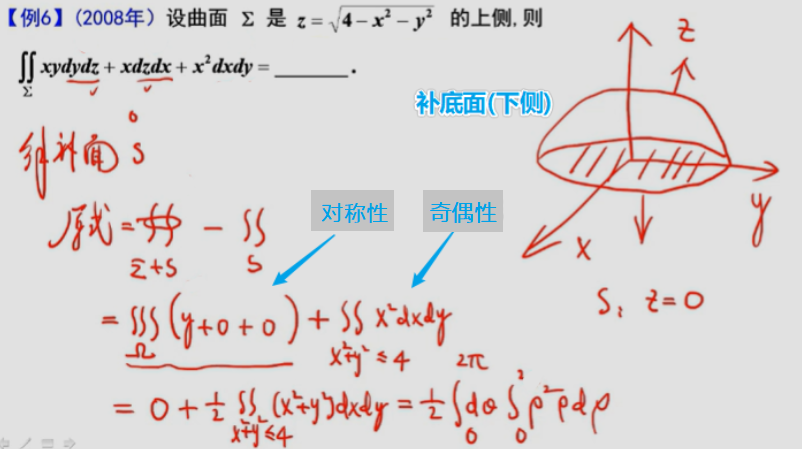

补下侧,此题积分是在内侧,而高斯公式是在外侧,所以要加负号
四、多元积分的应用
| 平面域 | 空间体 | 曲线段 | 曲面片 | |
|---|---|---|---|---|
| 几何度量 | 面积S=$\iint_D$dσ | 体积V=$\iiint_\Omega$dv | 弧长L=$\int_C$ds | 面积S=$\iint_\Sigma$dS |
| 质量 | m=$\iint_D $ρ(x,y)dσ | m=$\iiint_\Omega$ρ(x,y,z)dv | m=$\int_C$f(x,y,z)ds | m=$\iint_\Sigma$ρ(x,y,z)dS |
| 质心 | $\overline {x}$=$\frac{\iint_D xρ(x,y)dσ}{\iint_D ρ(x,y)dσ}$ | $\overline {x}$=$\frac{\iiint_\Omega xρ(x,y,z)dv}{\iiint_\Omega ρ(x,y,z)dv}$ | $\overline {x}$=$\frac{\int_C\ xρ(x,y,z)ds}{\int_C\ ρ(x,y,z)ds}$ | $\overline {x}$=$\frac{\iint_\Sigma xρ(x,y,z)dS}{\iint_\Sigma ρ(x,y,z)dS}$ |
| 转动惯量 | I$_x$ =$\iint_D $y² ρ(x,y)dσ | I$x$ =$\iiint\Omega $(y²+z²) ρ(x,y,z)dv | I$_x$ =$\int_C $(y²+z²) ρ(x,y,z)ds | I$x$ =$\iint\Sigma$(y²+z²) ρ(x,y,z)dS |
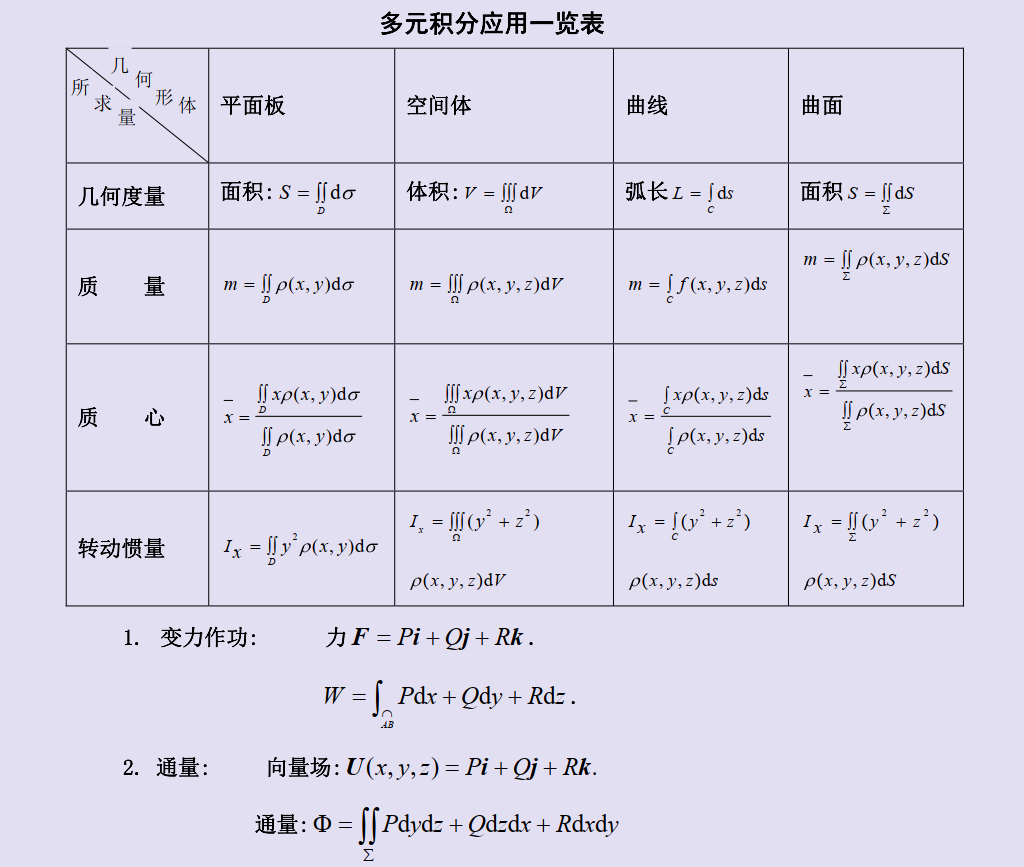
————题型归纳
形心和变力做功的计算
————典型例题



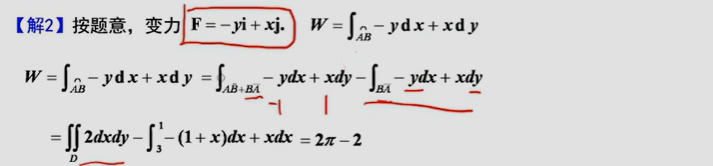
补线格林
五、场论初步
1、方向导数

cosα、cosβ为方向余弦
2、梯度
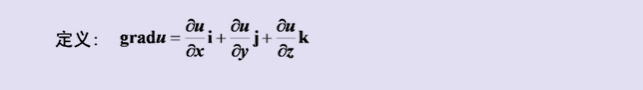
梯度gradf (x0 , y0 ) 是一个向量,它的方向是函数在这点方向导数最大的方向,它的模等于方向导数的最大值.
3、散度
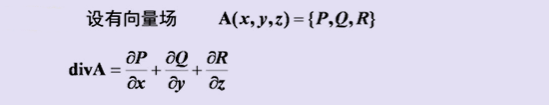
4、旋度

————典型例题


拉格朗日乘数法
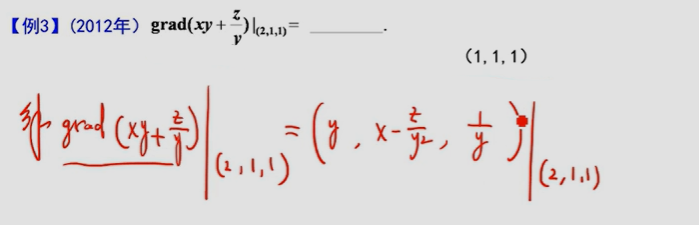
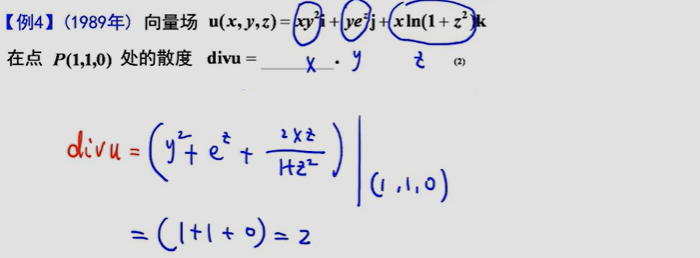
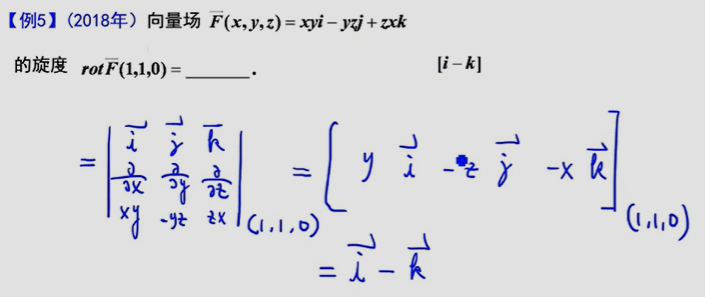
无穷级数
一、常数项级数
1、级数的概念



2、级数的性质


比如1,-1,1,-1,1,-1……收敛,但其Sn=(1,n为奇数;0,n为偶数)显然发散
加括号后将变成新级数,第一个即为第一项,第二个为第二项...
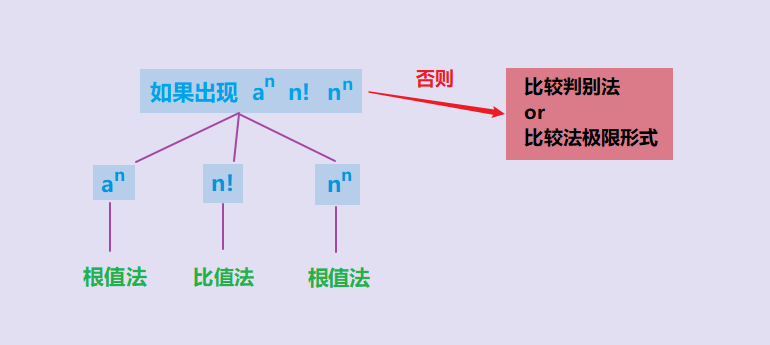
3、级数的审敛准则
(1)正项级数

注:只适用于正项级数,不适用与任意项级数

②:l=0说明un<vn,那么大的收敛小的就收敛

| 方法 | 优点 | 缺点 |
|---|---|---|
| 比较判别法、比较法极限形式 | 适用范围广 | 不方便 |
| 比值法、根值法 | 方便 | 适用范围小 |
(2)交错级数

(3)任意项级数

————题型归纳
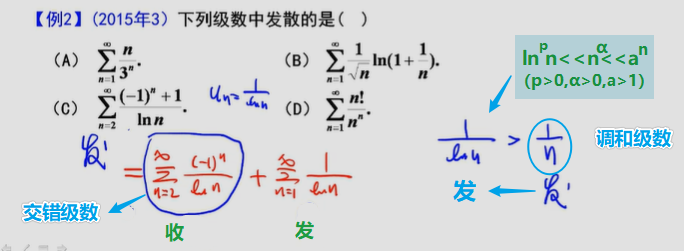
常数项级数敛散性判定
————典型例题



$$ \sum_{n=1}^∞|b_n| 收敛,且\lim_{n\rightarrow\infin} a_n=0 \Longrightarrow\sum_{n=1}^∞|a_nb_n|收敛 \ \sum_{n=1}^∞|a_n| 收敛 \Longrightarrow\sum_{n=1}^∞a_n^2收敛 $$

二、幂级数
1、幂级数的相关定义

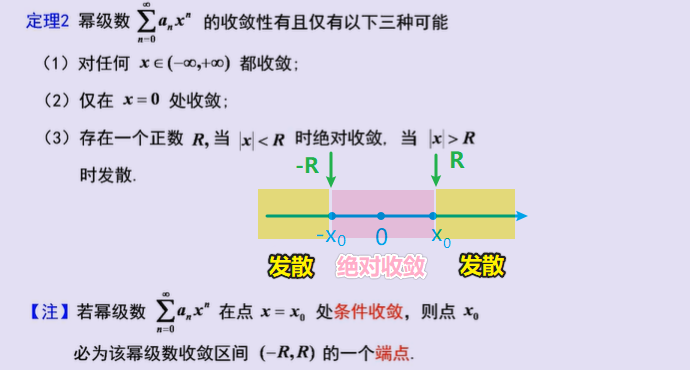
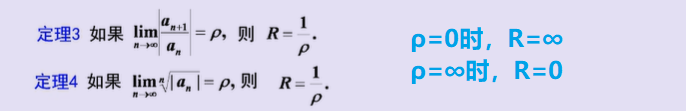
2、幂级数的性质



3、函数的幂级数展开


常用展开式:
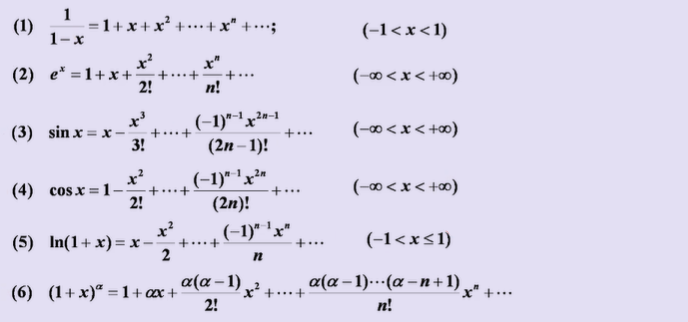
对sinx求导就是cosx
1/(1+x)=$\sum_{n=0}^{∞} (-1)^nx^n$
函数展开为幂级数的两种方法:

————题型归纳
- 求收敛半径、收敛区间及收敛域
- 将函数展开为幂函数
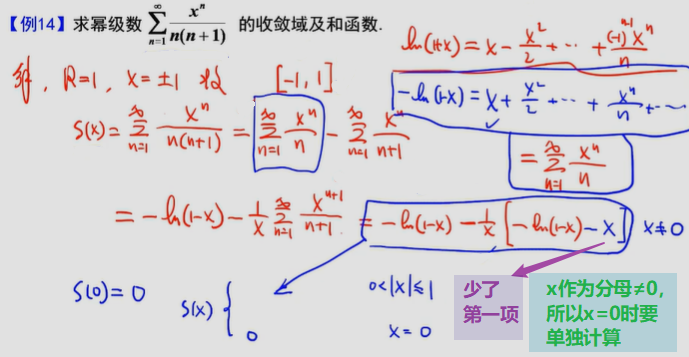
- (难) 级数求和
————典型例题
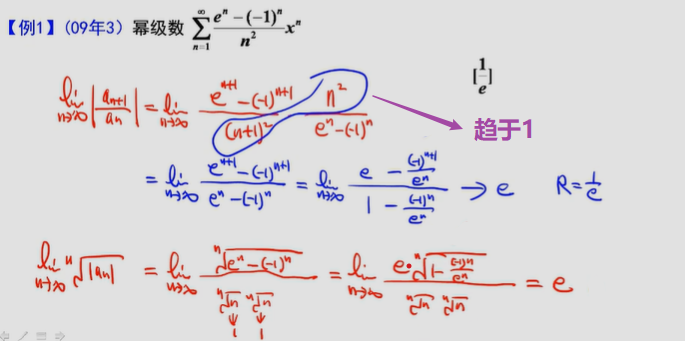
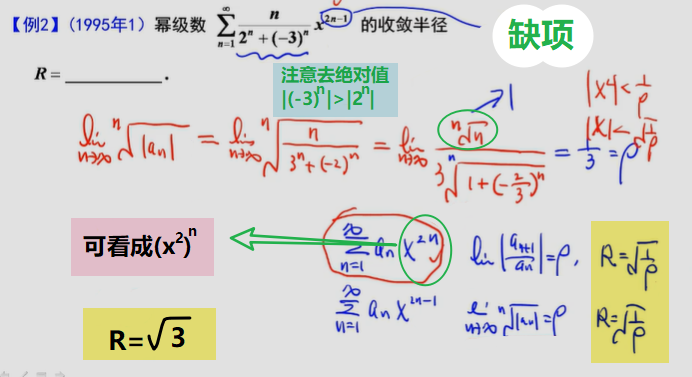

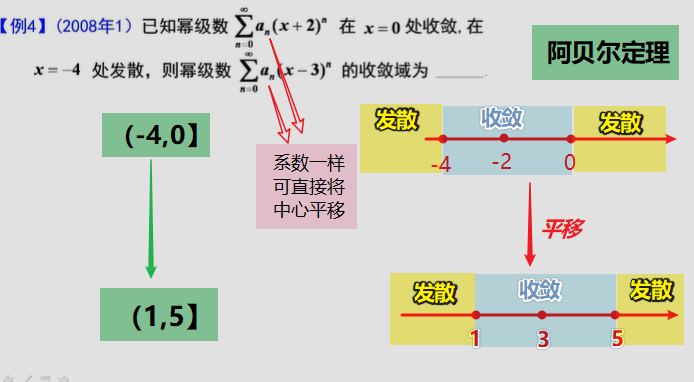
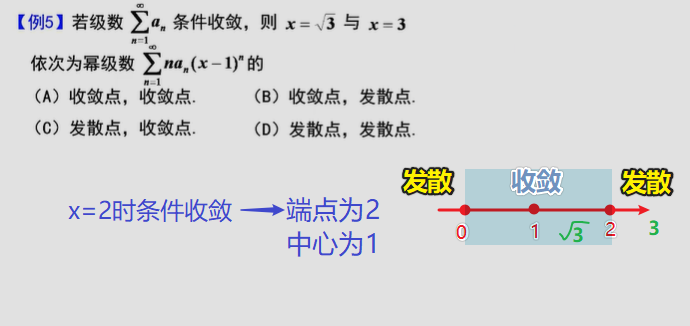
∵级数an条件收敛,那么x=2时幂级数nan(x-1)^n^条件收敛









三、傅里叶级数
1、傅里叶系数与傅里叶级数
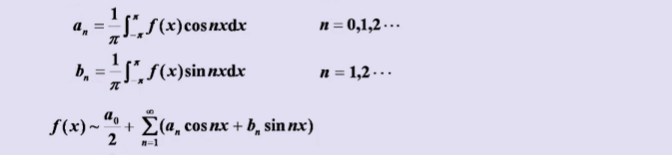
2、收敛定理(狄利克雷)

3、周期为2π的函数的展开


4、周期为2l的函数的展开
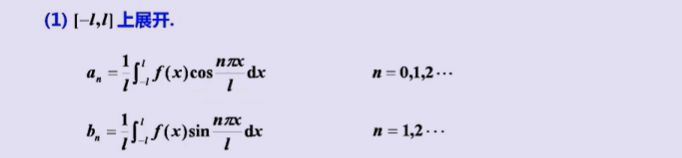


————题型归纳
- 狄利克雷收敛定理
- 将函数展开为傅里叶级数
————典型例题


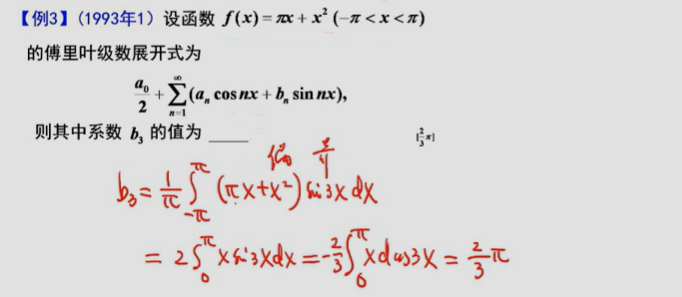

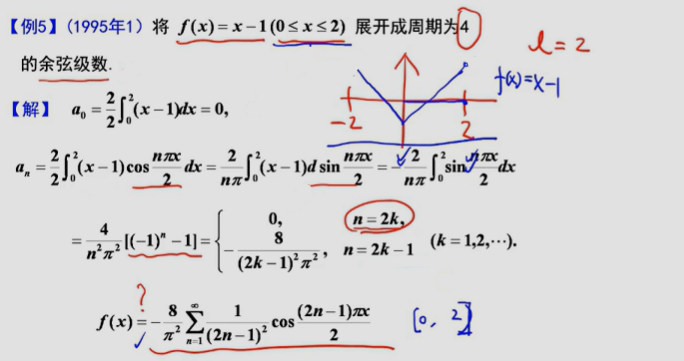
附录
常用公式
极限运算法则

常用基本极限


常用等价无穷小
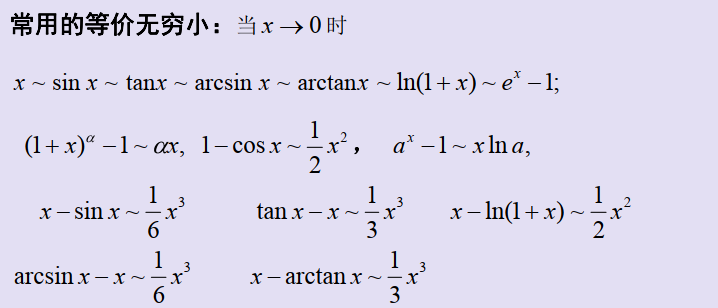
泰勒公式
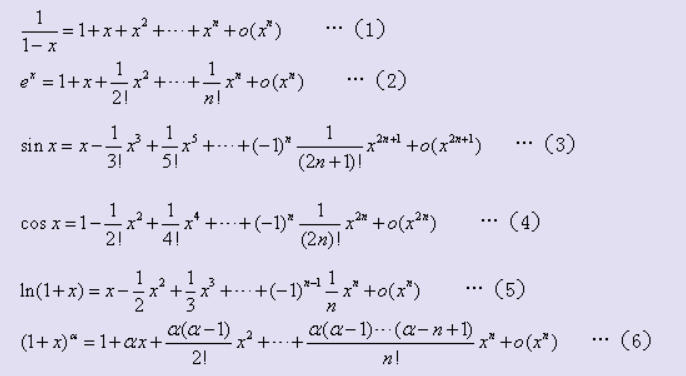
常用高阶导数公式
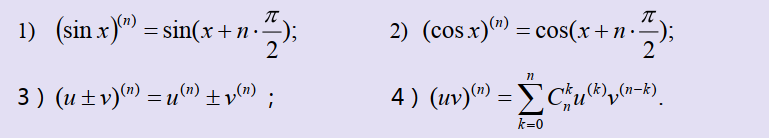
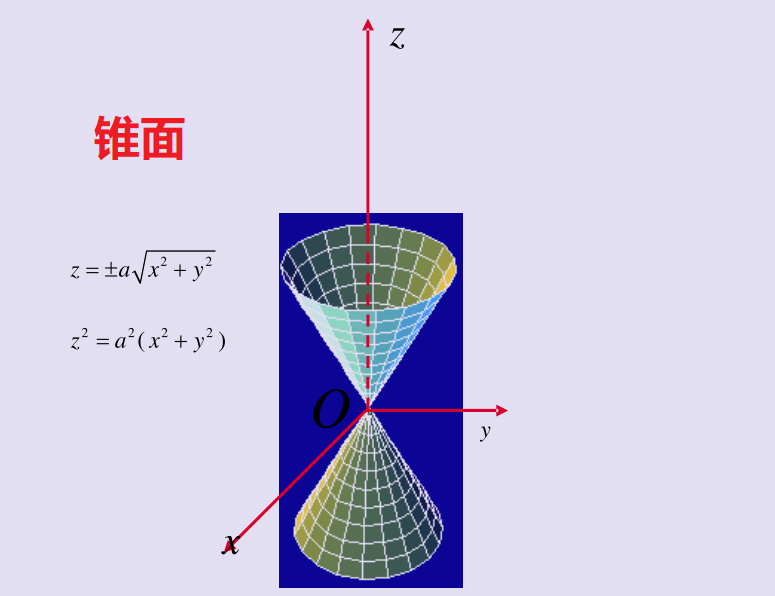
常见空间曲面方程
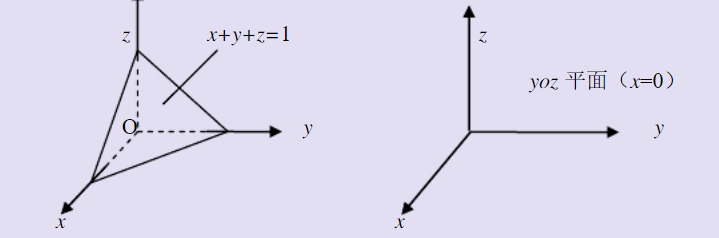
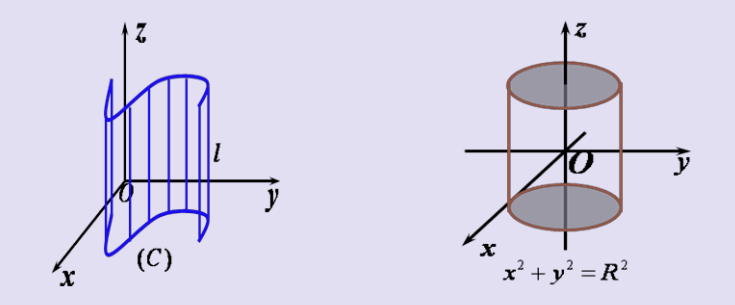
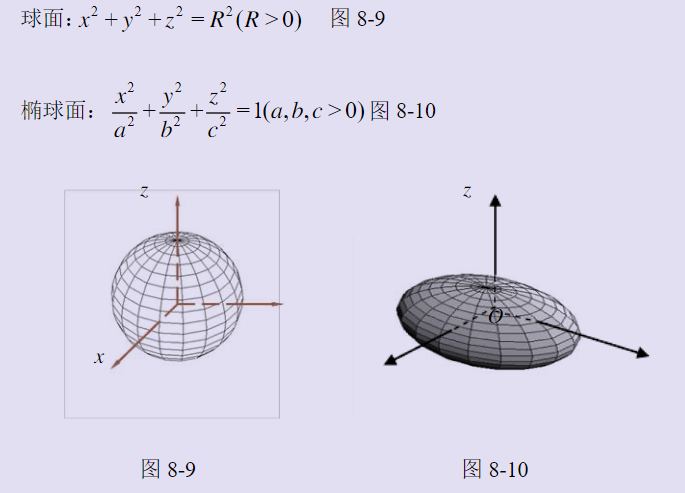
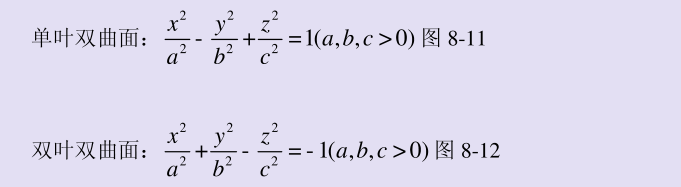
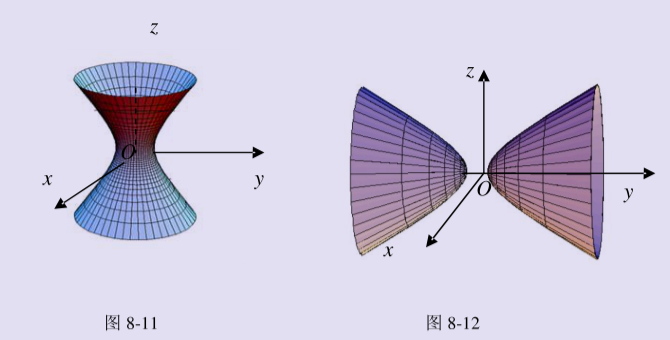
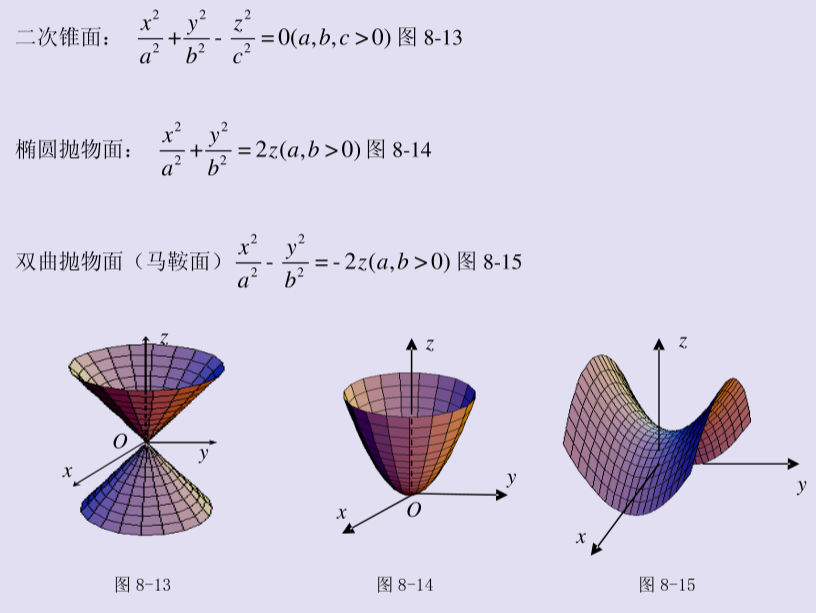
z=a(x²+y²)为旋转抛物面:即先写出z=ax²,将x更换为根号下x²+y²
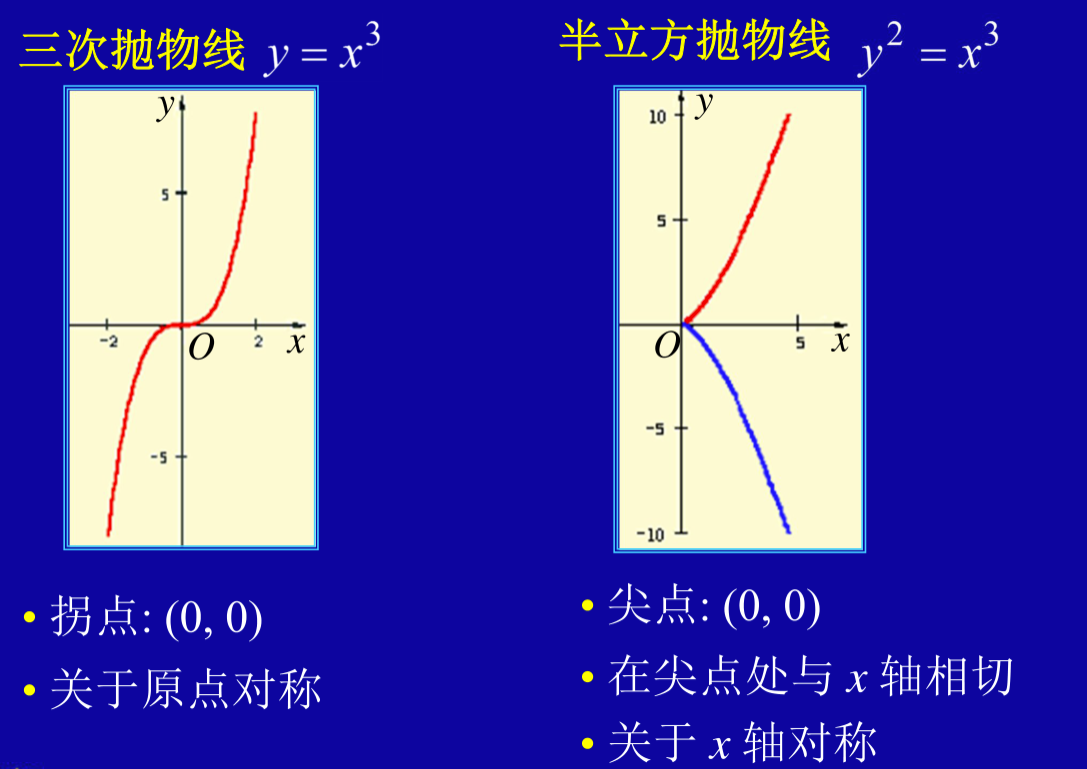
常见二维平面方程
抛物线
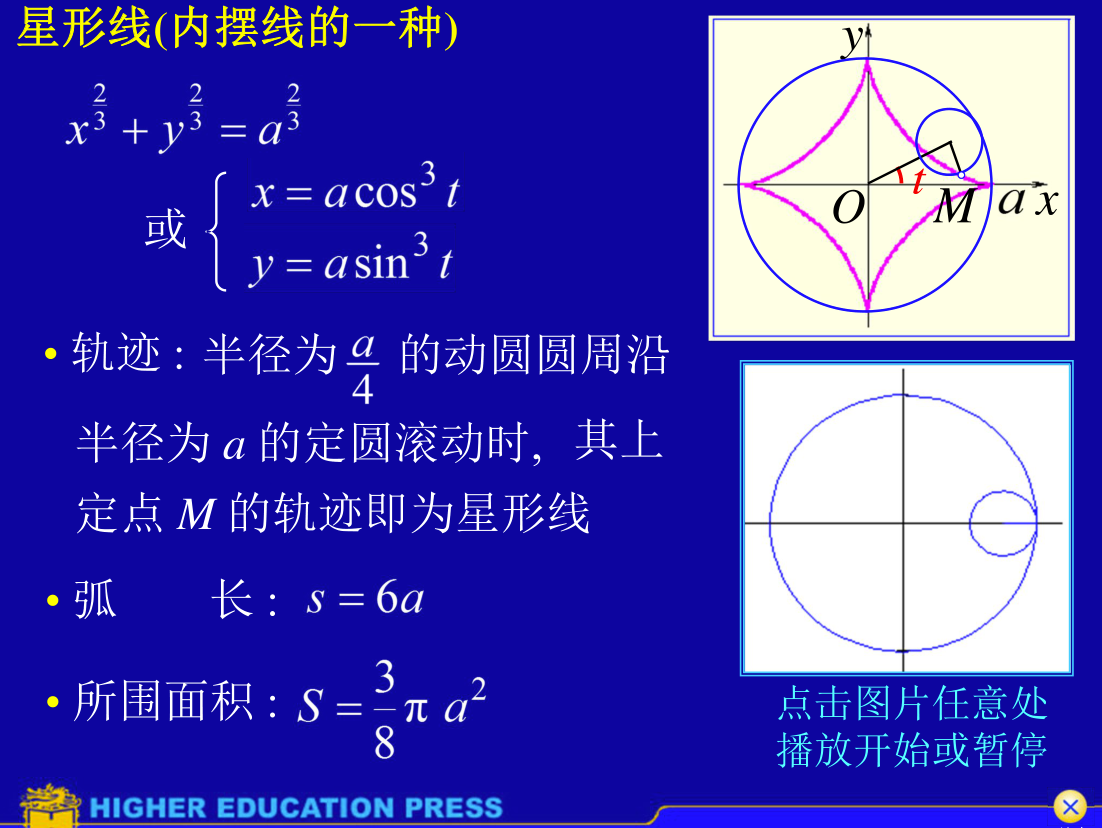
星形线
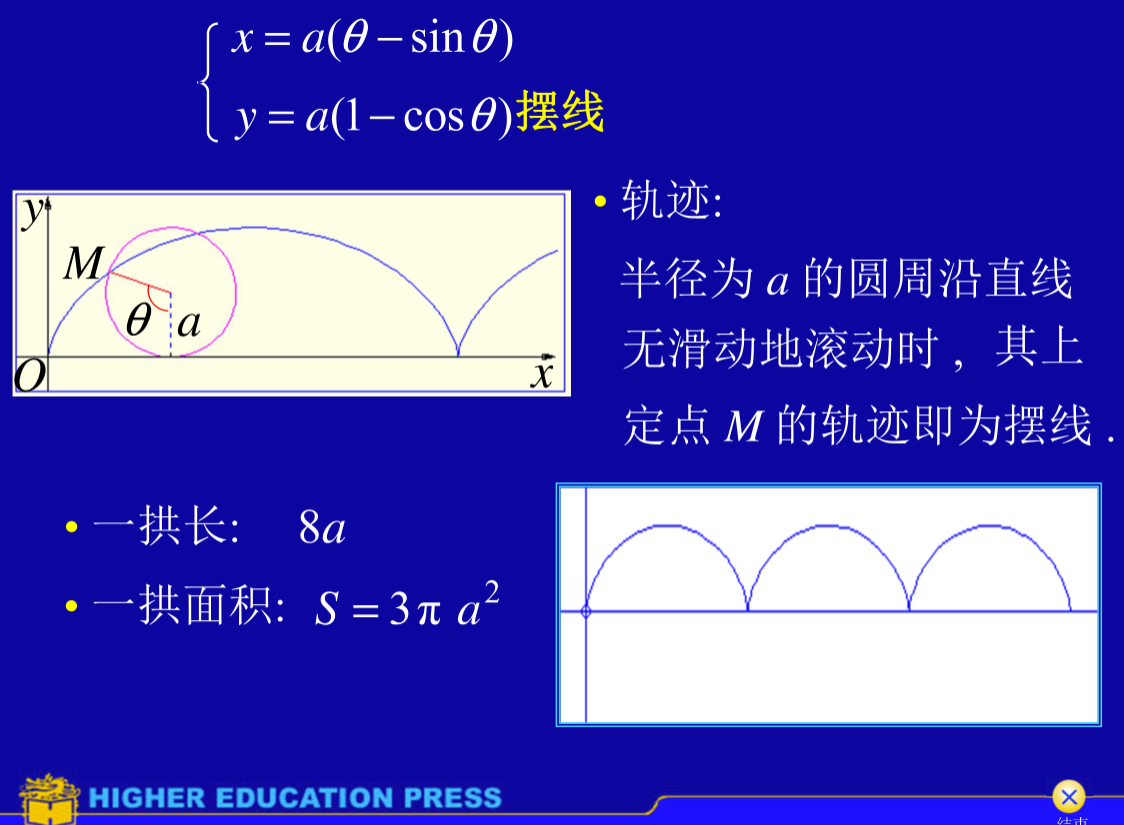
摆线
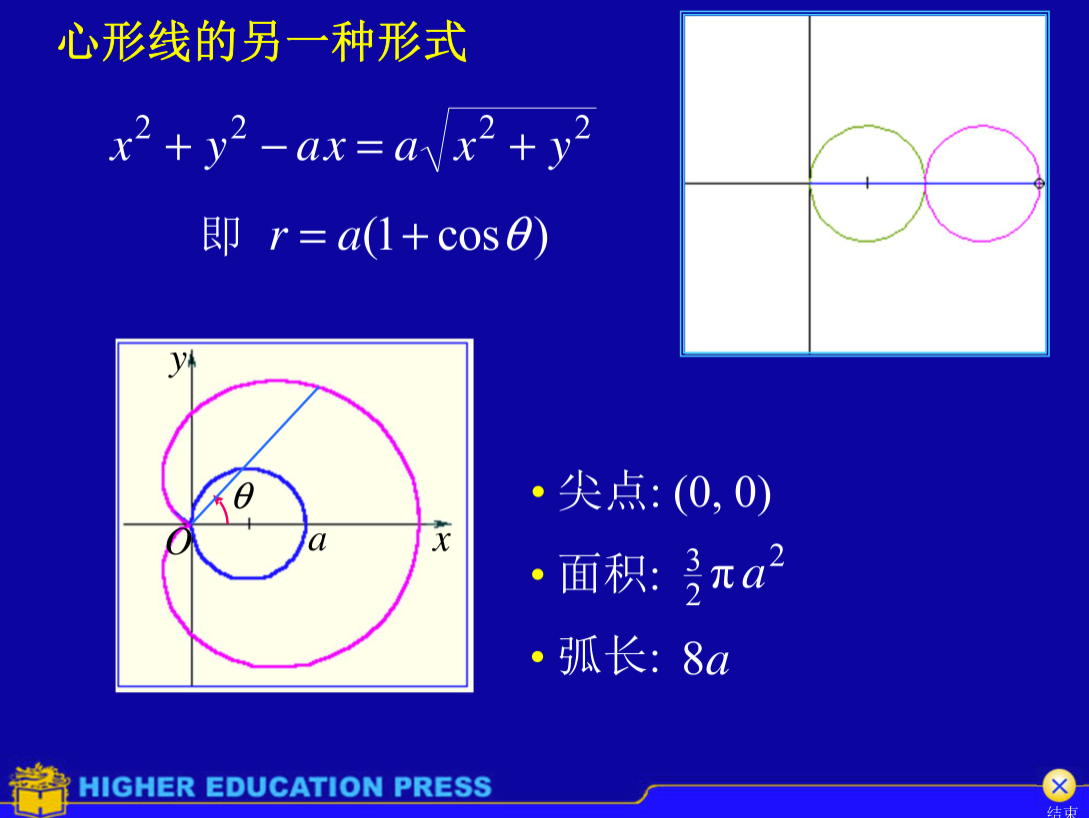
心形线

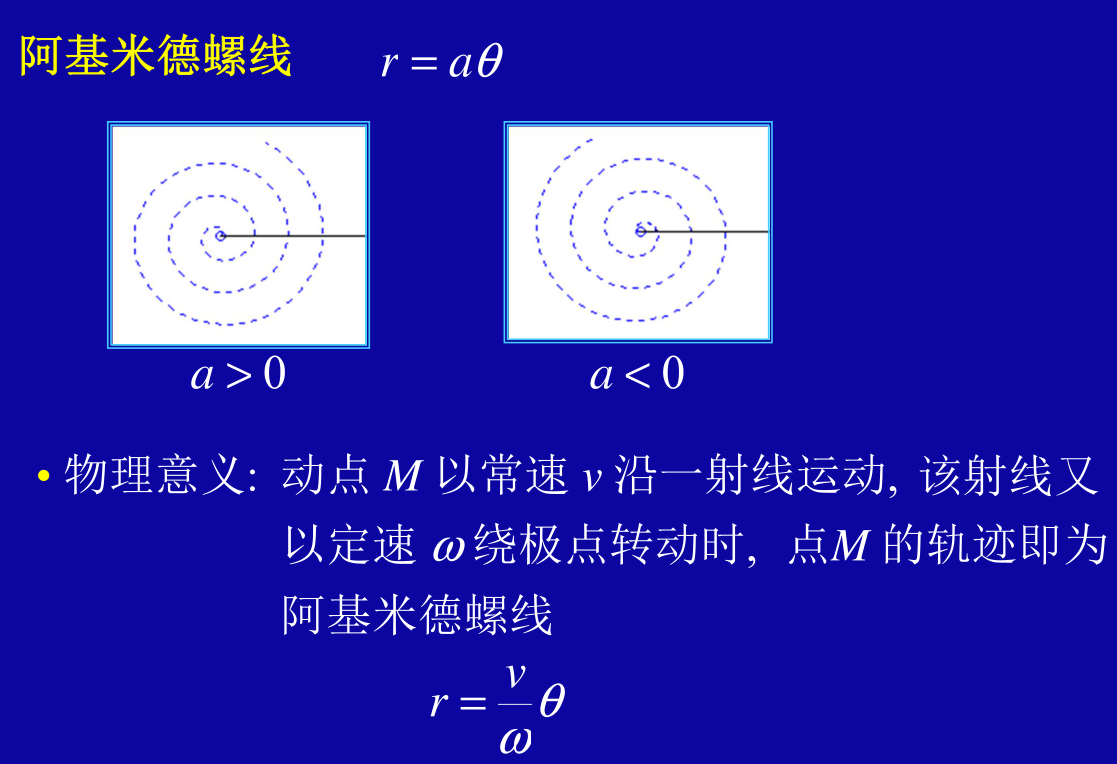
阿基米德螺线
伯努利双纽线

三叶玫瑰线


